Plus One Computer Science Chapter Wise Questions and Answers Chapter 2 Data Representation and Boolean Algebra

Students can Download Chapter 2 Data Representation and Boolean Algebra Questions and Answers, Plus One Computer Science Chapter Wise Questions and Answers helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus One Computer Science Chapter Wise Questions and Answers Chapter 2 Data Representation and Boolean Algebra

Plus One Data Representation and Boolean Algebra One Mark Questions and Answers

Question 1.
___________ is a collection of unorganized fact.
Answer:
Data

Question 2.
Data can be organized into useful ____________
Answer:
Information

Question 3.
___________ is used to help people to make decision.
Answer:
Information

Question 4.
Processing is a series of actions or operations that convert inputs into __________
Answer:
Output

Question 5.
The act of applying information in a particular context or situation is called ____________
Answer:
Knowledge

Question 6.
What do you mean by data processing?
Answer:
Data processing is defined as a series of actions or operations that converts data into useful information.

Question 7.
Odd man out and justify your answer.
(a) Adeline
(b) 12
(3) 17
(d) Adeline aged 17 years is in class 12.
Answer:
(d) Adeline aged 17 years is in class 12. This is information. The others are data.

Question 8.
Raw facts and figures are known as _______
Answer:
data

Question 9.
Processed data is known as _______
Answer:
Information

Question 10.
Which of the following helps us to take decisions?
(a) data
(b) information
(c) Knowledge
(d) intelligence
Answer:
(b) information

Question 11.
Manipulation of data to get information is known as ___________
Answer:
Data processing

Question 12.
Arrange the following in proper order
Process, Output, Storage, Distribution, Data Capture, Input.
Answer:

1. Data Capture
2. Input
3. Storage
4. Process
5. Output
6. Distribution

Question 13.
Pick the odd one out and give reason:
(a) Calculation
(b) Storage
(c) Comparison
(d) Categorization
Answer:
(b) Storage. It is one of the data processing stage the others are various operations in the stage Process

Question 14.
Information may act as data. State true or False.
Answer:
False

Question 15.
Complete the Series.

1. (101)₂, (111)₂, (1001)₂, ……….
2. (1011)₂, (1110)₂, (10001)₂, ………

Answer:

1. 1011, 1101
2. 10101, 10111

Question 16.
What are the two basic types of data which are stored and processed by computers?
Answer:
Characters and number

Question 17.
The number of numerals or symbols used in a number system is its _______________
Answer:
Base

Question 18.
The base of decimal number system is ________
Answer:
10

Question 19.
MSD is ________
Answer:
Most Significant Digit

Question 20.
LSD is _________
Answer:
Least Significant Digit

Question 21.
Consider the number 627. Its MSD is _________
Answer:
6

Question 22.
Consider the number 23.87. Its LSD is __________
Answer:
7

Question 23.
The base of Binary number system is ___________
Answer:
2

Question 24.
What are the symbols used in Binary number system?
Answer:
0 and 1

Question 25.
Complete the following series,
(101)₂, (111)₂, (1001)₂
Answer:
1011, 1101

Question 26.
State True or False. In Binary, the unit bit changes either from 0 to 1 or 1 to 0 with each count.
Answer:
True

Question 27.
The base of octal number system is ________
Answer:
8

Question 28.
Consider the octal number given below and fill in the blanks.
0, 1, 2, 3, 4, 5, 6, 7, __
Answer:
10

Question 29.
The base of Hexadecimal number system is ________
Answer:
16

Question 30.
State True or False.
In Positional number system, each position has a weightage.
Answer:
True

Question 31.
In addition to digits what are the letters used in Hexadecimal number system.
Answer:
A(10), B(11), C(12), D(13), E(14), F(15)

Question 32.
Convert (1110.01011)₂ to decimal.
Answer:
1110.01011 = 1 × 23 + 1 × 22 + 1 × 21 + 0 × 20 + 0 × 2 – 1 + 1 × 2 – 2 + 0 × 2 – 3 + 1 × 2 – 4 + 1 × 2 – 5
= 8 + 4 + 2 + 0 + 0 + 0.25 + 0 + 0.0625 + 0.03125
= (14.34375)10

Question 33.
1 KB is bytes.
(a) 2⁵
(b) 2¹⁰
(c) 2¹⁵
(d) 2²⁰
Answer:
(b) 2¹⁰

Question 34.
The base of hexadecimal number system is ________.
Answer:
16

Question 35.
A computer has no _________
(a) Memory
(b) l/o device .
(c) CPU
(d) IQ
Answer:
(d) IQ

Question 36.
Pick the odd man out.
(AND, OR, NAND, NOT)
Answer:
NOT

Question 37.
Select the complement of X + YZ.
(a) \(\bar{x}+\bar{y}+\bar{z}\)
(b) \(\bar{x} .\bar{y}+\bar{z}\)
(c) \(\bar{x} \cdot(\bar{y}+\bar{z})\)
(d) \(\bar{x}+\bar{y} \cdot \bar{z}\)
Answer:
(c) \(\bar{x} \cdot(\bar{y}+\bar{z})\)

Question 38.
Select the expression for absorption law.
(a) a + a = a
(b) 1 + a = 1
(c) o . a = 0
(d) a + a . b = a
Answer:
(a) a + a . b = a

Question 39.
What is the characteristic of logical expression?
Answer:
Logical expressions yield either true or false values

Question 40.
Name the table used to define the results of Boolean operations.
Answer:
Truth Table

Question 41.
According to ________ law, \(\bar{x}+\bar{y}=\overline{x y}\) and \(\overline{x y}=\bar{x}+\bar{y}\)
Answer:
De Morgan’s law

Question 42.
A NOR gate is ON only when all its inputs are
(a) ON
(b) Positive
(c) High
(d) OFF
Answer:
(d) OFF

Question 43.
The only function of a NOT gate is __________
Answer:
Invert an output signal

Question 44.
NOT gate is also known as _________
Answer:
Inverter

Question 45.
What is the relation between the following statements.
x + 0 = x and x . 1 = x
Answer:
One is the dual of the other expression.

Question 46.
The algebra used to solve problems in digital systems is called __________
Answer:
Boolean Algebra

Question 47.
Pick the one which is not a Basic Gate.
(AND, OR, XOR, NOT)
Answer:
XOR

Question 48.
Select the universal gates from the list. (NAND, NOR, NOT, XOR)
Answer:
NAND, NOR

Question 49.
Which is the final stage in data processing?
Answer:
Distribution of information is the final stage in data processing

Question 50.
Fill up the missing digit.
(41)₈ = ( )₁₆
Answer:

• Step 1: Divide the number into one each and write down the 3 bits equivalent.
• Step 2: Then divide the number into group of 4 bits starting from the right then write its equivalent hexa decimal.

Answer:
So the answer is 21.

Question 51.
Real numbers can be represented in memory by using __________
Answer:
Exponent and Mantissa

Question 52.
Consider the number 0.53421 x 10^-8 Write down the mantissa and exponent.
Answer:
Mantissa: 0.53421
Exponent: -8

Question 53.
Characters can be represented in memory by using _________
Answer:
ASCII Code

Question 54.
ASCII Code of A’ is __________
Answer:
(100 0001)₂ = 65

Question 55.
ASCII Code of’a’ is __________
Answer:
(110 0001)₂ = 97

Question 56.
Define the term ‘bit’?
Answer:
A bit stands for Binary digit. That means either 0 or 1.

Question 57.
Find MSD in the decimal number 7854.25
Answer:
Because it has the most weight

Question 58.
ASCII stands for __________.
Answer:
American Standard Code for Information Interchange

Question 59.
List any two image file formats.
Answer:
BMP, GIF

Question 60.
Name the operator which performs logical multiplication.
Answer:
AND

Question 61.
Name a gate which is ON when all its inputs are OFF .
Answer:
NAND or NOR

Question 62.
Specify the laws applied in the following cases.

1. a (b + c) = ab + ac
2. (a + b) + c = a + (b + c)

Answer:

1. Distribution law
2. Associative law

Question 63.
Pick the correct Boolean expression from the following.
(a) \(A +\bar{A}=163.\)
(b) \(\text { A. } \bar{A}=1\)
(c) \(A \cdot \overline{A B}=A + B\)
(d) A + AB = A
Answer:
(a) & (d)

Question 64.
1’s complement of the binary number 110111 is _________
Answer:
Insert 2 zeroes in the left hand side to make the binary number in the 8 bit form 00110111
To find the 1’s complement, change all zeroes to one and all ones to zero. Hence the answer is 11001000

Plus One Data Representation and Boolean Algebra Two Mark Questions and Answers

Question 1.
Why do we store information?
Answer:
Normally large volume of data has to be given to the computer for processing so the data entry may be taken more days, hence we have to store the data. After processing these stored data, we will get information as a result that must be stored in the computer for future references.

Question 2.
What is source document.
Answer:
Acquiring the required data from all the sources for the data processing and by using this data design a document, that contains all relevant data in proper order and format. This document is called source document.

Question 3.
Briefly explain data, information and processing with real life example.
Answer:
Consider the process of making coffee. Here data is the ingredients – water, sugar, milk and coffee powder
Information is the final product i.e. Coffee Processing is the series of steps to convert the ingredients into final product, Coffee. That is mix the water,sugar and milk and boil it. Finally pour the coffee powder.

Question 4.
ASCII is used to represent characters in memory. Is it sufficient to represent all characters used in the written languages of the world? Propose a solution. Justify.
Answer:
No It is not sufficient to represent all characters used in the written languages of the world because it is a 7 bit code so it can represent 2⁷ = 128 possible codes. To represent all the characters Unicode is used because it uses 4 bytes, so it can represent 232 possible codes.

Question 5.
The numbers in column A have an equivalent number in another number system of column B.
Find the exact matvh

A	B
(12)8	(1110)2
F16	25
(19)16	10
(11)8	(13)16
	(17)8
	9

Answer:

A	B
12	10
F	(17)8
(19)16	25
(11)8	9

Question 6.

1. Name various number systems commonly used in computers.
2. Include each of the following numbers into all possible number systems
   123 569 1101

Answer:

1. The number system are binary, octal, decimal and hexa decimal
2. All possible number systems are
   • 123 Octal, decimal and hexa decimal
   • 569 Decimal, hexa decimal
   • 1101 Binary, Octal, Decimal, Hexa decimal

Question 7.
Fill up the missing digit. (Score 2)
If (220)_a = (90)_b then (451)_a = (  )₁₀
Answer:
It contains 2 & 9, so a and b 2, b 8. The values of a can be 8 or 10. The values of b can be 10 or 16. L.H.S > R.H.S. a < b and a b also.
The possible values of a and b are given below.

Question 8.
Convert (106)₁₀ = (  )₂?
Answer:

Question 9.
Convert (106)₁₀ = (  )₈?
Answer:

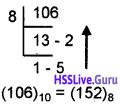
Question 10.
(106)₁₀ = (  )₁₆?
Answer:

Question 11.
Convert (55.625)₁₀ = (  )₂?
Answer:
First convert 55, for this do the following

Write down the remainders from bottom to top.
(55)₁₀ = (110111 )₂
Next convert 0.625, for this do the following.

Write down the remainder from top to bottom. So the answer is
(55.625)₁₀ = (110111.101)₂

Question 12.
Convert (55.140625)₁₀ = (  )₈?
Answer:
First convert 55, for this do the following.

Write down the remainders from bottom to top.
(55)₁₀ = (67)₈
Next convert 0.140625, for this do the following.

Write down the remainders from top to bottom. So the answer is
(55.140625)₁₀ = (67.11 )₈

Question 13.
Convert (55.515625)₁₀ = (  )₁₆
Answer:
First convert 55, for this do the following.

Write down the remainders from bottom to top.
ie. (55)₁₀ = (37)₁₆
Next convert .515625

So the answer is
(55.515625)₁₀ = (37.84)₁₆

Question 14.
Convert (101.101)₂ = ( )₁₀?
Answer:
101.101 = 1 × 2² + 0 × 2¹ + 1 × 2⁰ + 1 × 2^-1 + 0 × 2^-2 + 1 × 2^-3 = 4 + 0 + 1 + 1/2 + 0 + 1/8 = 5 + 0.5 + 0.125
(101.101)₂ = (5.625)₁₀

Question 15.
Convert (71.24)₈ = (  )₁₀?
Answer:
71.24 = 7 × 8¹ + 1 × 8⁰ + 2 × 8^-1 + 4 × 8⁼²
= 56 + 1 + 2/8 + 4/82
= 57 + 0.25 + 0.0625 (71.24)8
(71.24)₈ = (57.3125)₁₀

Question 16.
Convert (AB.88)₁₆ = (  )₁₀?
Answer:

= 160 + 11 + 0.5 + 0.03125
(AB.88)₁₆ = (171.53125)₁₀

Question 17.
Convert (1011)₂ = (  )₈?
Answer:
Step I: First divide the number into groups of 3 bits starting from the right side and insert necessary zeroes in the left side.
0 0 1 | 0 1 1

Step II: Next write down the octal equivalent.

So the answer is (1011)₂ = (13)₈.

Question 18.
Convert (110100)₂ = (  )₁₆
Answer:

• Step I: First divide the number into groups of 4 bits starting from the right side and insert necessary zeroes in the left side.
• Step II: Next write down the hexadecimal equivalent.

So the answer is (110100)₂ = (34)₁₆.

Question 19.
(72)₈ = ( )₂?
Answer:
Write down the 3 bits equivalent of each digit.

So the answer is (72)₈ = (111010)₂.

Question 20.
Convert (AO)₁₆ = (  )₂ ?
Answer:
Write down the 4 bits equivalent of each digit

So the answer is (AO)₁₆ = (1010 0000)₂.

Question 21.
Convert (67)₈ = (  )₁₆?
Answer:
Step I: First convert this number into binary equivalent for this do the following

Step II: Next convert this number into hexadecimal equivalent for this do the following.

So the answer is (67)₈ = (37)₁₆

Question 22.
Convert (A1)₁₆ = (  )₈?
Answer:
Step I: First convert this number into binary equivalent. For this do the following

Step II: Next convert this number into octal equivalent. For this do the following.

So the answer is (A1)₁₆ = ( 241)₈.

Question 23.
What is the use of the ASCII Code?
Answer:
ASCII means American Standard Code for Information Interchange. It is a 7 bit code. Each and every character on the keyboard is represented in memory by using ASCII Code.
eg: A’s ASCII Code is 65 (1000001), a’s ASCII Code is 97 (1100001)

Question 24.
Pick invalid numbers from the following.

1. (10101)₈
2. (123)₄
3. (768)₈
4. (ABC)₁₆

Answer:

1. (10101)₈ – Valid
2. (123)₄ – Valid
3. (768)₈ – Invalid. Octal number system does not contain the symbol 8
4. (ABC)₁₆ – Valid

Question 25.
Convert the decimal number 31 to binary.
Answer:

(31)₁₀ = (11111)₂

Question 26.
Find decimal equivalent of (10001 )₂
Answer:

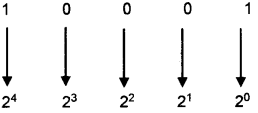
= 1 × 24 + 0 × 23 + 0 × 22 + 0 × 21 + 1 × 20
= 16 + 0 + 0 + 0 + 1
= (17)₁₀

Question 27.
If (X)₈ =(101011 )₂ then find X.
Answer:
Divide the binary number into groups of 3 bits and write down the corresponding octal equivalent.

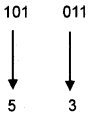
X = 53

Question 28.
Fill the blanks:
(a) (………..)₂ = (AB)₁₆
(b) (——D—–)₁₆ = (1010 1000)₂
(c) 0.25₁₀ = (—–)₂

Answer:
Write down the 4bit equivalent of each digit
(a) (………..)₂ = (AB)₁₆

= (10101011)₂
(b) (——D—–)₁₆ = (1010 1000)₂
(A D 8)₁₆ =(1010 1101 1000)₂

(c) 0.25₁₀ = (—–)₂

0.25₁₀ = (0.01)₂

Question 29.
Which is the MSB of representation of -80 in SMR?
Answer:
It is 1 because In SMR if the number is negative then the MSB is 1.

Question 30.
Write 28.756 in Mantissa exponent form.
Answer:
28.756 = .28756 × 100
= .28756 × 102
= .28756 E + 2

Question 31.
Represent -60 in 1’s complement form.
Answer:
+60 = 00111100
Change all 1 to 0 and all 0 to 1 to get the 1’s complement.
-60 is in 1’s complement is 11000011

Question 32.
Define Unicode.
Answer:
The limitations to store more characters is solved by the introduction of Unicode. It uses 16 bits so 2¹⁶ = 65536 characters(i.e, world’s all written language characters) can store by using this.

Question 33.
Substract 1111 from 10101 by using 2’s complement method.
Answer:
To subtract a number from another number find the 2’s complement of the subtrahend and add it with the minuend. Here the subtrahend is 1111 and minuend is 5 bits. So insert a zero. So subtrahend is 01111. First take the 1’s complement of subtrahend and add 1 to it

Here is a carry. So ignore the carry and the result is +ve.
So the answer is 110

Question 34.
You purchased a soap worth Rs. (10010)₂ and you gave Rs. (10100)₂ and how much rupees will you get back in binary.
Answer:
Substract (10010)₂ from (10100)₂

You will get rupees (10)₂

Question 35.
Draw the logic circuit diagram for the following Boolean expression.
Answer:

Question 36.
Simplify the expression using basic postulates and laws of Boolean algebra.

1. \(\bar{x}+x \cdot \bar{y}\)
2. \(x(y+y . z)+y(\bar{x}+x z)\)

Answer:

1. \(\bar{x}+\bar{y}\)
2. y

Question 37.
Show \(A(\bar{B}+C)\) using NOR gates only.
Answer:

Question 38.
The following statement Demorgan’s theorem of Boolean algebra. Identify and state ‘Break the line, change the sign’.
Answer:
Demorgan’s theorems,
Demorgan’s first theorem,
\(\overline{x + y}\) = \(\bar{x} . \bar{y}\)
Demorgan’s second theorem,
\(\overline{x – y}\) = \(\bar{x} + \bar{y}\)

Question 39.
Prove algebraically that
\(x \cdot y + x \cdot \bar{y} \cdot z\) = x . y + x . z
Answer:
\(x \cdot y + x \cdot \bar{y} \cdot z\) = \(x(y+\bar{y} . z)\)
= x . (y + z) = x . y + x . z
Hence proved.

Question 40.
State which of the following statements are logical statements.
(a) AND is a logical operator
(b) ADD 3 to y
(c) Go to class
(d) Sun rises in the west.
(e) Why are you so late?
Answer:
(a) and (d) are logical statements because these statements have a truth value which may be true or false.

Question 41.
Express the integer number -39 in sign and magnitude represnetation.
Answer:
First find the binary equivalent of 39 for this do the following

In sign and magnitude representation -39 in 8 bit form is (10100111)₂.

Question 42.

1. Which logic gate does the Boolean expression \(\overline{\mathrm{AB}}\) represent?
2. Some NAND gates are given. How can we construct AND gate, OR gate and NOT gate using them?

Answer:
1. NAND

2. AND gate

Question 43.
Perform the following number conversions.

1. (110111011.11011)₂ = (….)₈
2. (128.25)₁₀= (…..)₈

Answer:
1. 110111011.11011
Step 1: Insert a zero in the right side of the above number and divide the number into groups of 3 bits as follows
110 111 011 . 110 110

Step 2: Write down the corresponding 3 bit binary equivalent of each group
6 7 3 .6 6
Hence the result is (673.66)₈

2. It consists of 2 steps.
Step 1: First convert 128 into octal number for this do the following

Write down the remainders from bottom to top.
(128)₁₀ = (200)₈

Step 2: Then convert .25 into octal number for this do the following

(0.25)₁₀ = (0.2)₈.
Combine the above two will be the result.
(128.25)₁₀= (200.2)₈

Question 44.
Represent -38 in 2’s complement form.
Answer:
+38 = 00100110
First take the 1 ’s complement for this change all 1 to 0 and all 0 to 1

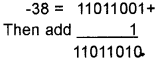
2’s complement of -38 is (11011010)₈.

Plus One Data Representation and Boolean Algebra Three Mark Questions and Answers

Question 1.
Differentiate manual data processing and electronic data processing?
Answer:
In manual data processing human beings are the processors. Our eyes and ears are input devices. We get data either from a printed paper, that can be read using our eyes or heard with ears. Our brain is the processor and it can process the data, and reach in a conclusion known as result. Our mouth and hands are output devices.

In electronic data processing the data is processing with the help of a computer. In a super market, key board and hand held scanners are used to input data, the CPU process the data, monitor and printers (Bill) are output devices.

Question 2.
Complete the series.

1. 3248, 3278 ,3328, …., ….
2. 5678, 5768, 605s, ……, …..

Answer:
1. (324)₈ = 3 × 82 + 2 × 81 + 4 × 80
= 3 × 64 + 2 × 8 + 4 × 1
= 192 + 16 + 4 = (212)10

(327)₈ = 3 × 82 + 2 × 81 + 7 × 80
= 192 + 16 + 7 = (215)₁₀

(332)₈= 3 × 82 + 3 × 81 +2 × 80
= 192 + 24 + 2 = (218)₁₀
So the missing terms are (221)₁₀, (224)₁₀ we have to convert this into octal.

So the missing terms are (335)₈, (340)₈

2. (567)₈ = 5 x 82 + 6 x 81 + 7 x 80
= 5 x 64 + 6 x 8 + 7 x 1
= 320 + 48 + 7 = (375)₁₀

(576)₈ = 5 x 82 + 7 x 81 + 6 x 80
= 320 + 56 + 6 = (382)₁₀

(605)₈ = 6 x 82 + 0 x 81 + 5 x 80
= 6 + 64 + 0 + 5
= 384 + 0 + 5 = (389)₁₀
So the missing terms are (396)₁₀, (403)₁₀ we have to convert this into octal.

So the missing terms are (614)₈, (623)₈

Question 3.
Fill up the missing digits.

1. (4……)₈ = (……110)₂
2. (…….7……)₈ = (100…….110)₂

Consider the following

Answer:
1. 4…….100 and 110……….6
So (46)₈ = (100 110)₂

2. 100…….4
7……111
110………6
So (476)₈ = (100 111 110)₂

Question 4.
Fill up the missing numbers.

1. (A…….)₁₆ = (……..1001)₂
2. (…….B…….)₁₆ = (1000………1111)₂

Consider the following:


Answer:
1. A……..1010
1001………9
So (A9)₁₆ = (1010 1001)₂

2. B…….1011
1000………8
1111………F
So (8BF)₁₆ = (1000 1011 1111)₂

Question 5.
Complete the Series.

1. 6ADD, 6ADF, 6AE1, ……., …….
2. 14A9, 14AF, 14B5, …….., ……

Answer:
1. Consider the sequence
6ADD, 6ADF, 6AE1, ………….
Here the ‘numbers’ are
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11,——–
The difference between 6ADD & 6ADF is 2

Similarly 6ADF & 6AE1 is 2

So Add 2 to 6AE1 we will ge 6AE3 Then add 2 to 6AE3 we will get 6AE5 Therefore the missing terms 6AE3, 6AE5

2. Consider the sequence.
14A9, 14AF, 14B5, ———
The difference between 14A9 and 14AF is 6.
The normal sequence is

The difference between 14AF and 14B5 is also 6.

The normal sequence is

Similarly the next 6 terms in the sequence are given below.

Similarly the next 6 terms are

So the missing terms are 14BB and 14C1

Question 6.
Find the octal numbers corresponding to the following numbers using shorthand method.

1. (ADD)₁₆
2. (DEAD)₁₆

Answer:
1. (ADD)₁₆
Step 1: Write down the 4 bit binary equivalent of each digit

Step 2: Divide this number into groups of 3 bits starting from the right and write down the octal equivalent.

(ADD)(ADD)₁₆ = (5335)(ADD)₈

2. (DEAD)₁₆
Step 1: Write down the 4 bit binary equivalent of each digit.

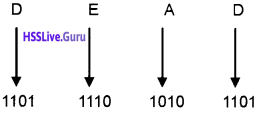
Step 2: Divide this number into groups of 3 bits starting from the right and write down the octal equivalent.

(DEAD)₁₆ = (157255)₈

Question 7.
If (126)x = (56)y, then find x and y.
Answer:
L.H.S contains 2 & 6, so x ≠ 2
R.H.S contains 5 & 6, so y ≠ 2
L.H.S > R.H.S
So x < y and x ≠ y also The possible values of x and y are given below.

Case I:
Let x = 8 then y = 10

It is grater than (56)₁₀
so when x = 8 then y ≠ 10

case II:
let x = 8 and y = 16

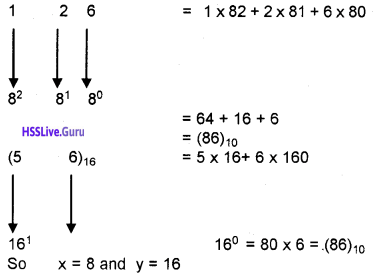
Question 8.
If (102)x = (42)y then (154)x = (  )y.
Answer:
L.H.S contains 2, so x ≠ 2
R.H.S contains 5 & 4, so y ≠ 2
L.H.S > R.H.S
So x < y and x ≠ y also
The possible values of x and y are given below.

case I:
let x = 8 and y = 10

So when x = 8 then y ≠ 10

case II:
let x = 8 and y = 16

So x = 8 and y = 16
then we have fo find the hexadecimal equivalent of (154)₈ For this first convert this into binary thus again convert it into hexadecimal. First write down the 3 bit equivalent of 154.

Then divide this number into groups of 4 bits starting from the right and write down the hexa decimal equivalent.

so the result is (154)₈ = (6C)₁₆

Question 9.
Fill up the missing digit.
If (121)_a = (441)_b then (121)_b = (  )₁₀
Answer:
L.H.S. contains 2, so a ≠ 2
R.H.S. contains 4, so b ≠ 2
L.H.S. < R.H.S. So a > b and a b also.
Hence the values of a can be 10 or 16.
The values of b can be 8 or 10.
The possible values of a and b are given below.

Case I:
Let a = 16 and b = 10
(121 )₁₆ = (289)_10, so b ≠ 10

Case II:
Let a = 16 and b = 8
(121)₁₆ = (289)₁₀
(441)₈ = 4 × 8² + 4 × 8¹ + 1 × 8⁰
= 256 +32 + 1
= (289)₁₀.
So a = 16 and b = 8.
Then (121)₈ = 1 × 82 + 2 × 81 + 1 × 80
= 64 + 16 + 1 = (81)₁₀

Question 10.
Fill up the missing digit. (Score 3)
If (128)_a = (450)_b then (16)_a = (  )₁₀
Answer:
L.H.S. contains 2 & 8, so a 2 and a ≠ 8.
R.H.S. contains 4 and 5, so b ≠ 2.
L.H.S. < R.H.S. so a > b and a ≠ b also.
The possible values of a and b are given below.

Case I:
a = 16 and b = 8
(128)₁₆ = (296)₁₀
(450)₈ = (296)₁₀ So a = 16 and b = 8.
Then (16)₁₆ = 1 × 16 + 6 × 16⁰ = (22)₁₀

Question 11.
Fill up the missing digit.
(3A.6D)₁₆ = (  )₈
Answer:
Step I: Write down the 4 bits equivalent of each digit.

Step II: Divide this number into groups of 3 bit starting from the right side of the left side of the decimal point and starting from the left side of the right side of the decimal point.
So 00/111/010.011/011/010

Step III: Write the octal equivalent of each group. SO we will get. (72.332)₈.
(3A.6D)₁₆ = (72.332)₈

Question 12.
What are the various ways to represent integers in computer?
Answer:
There are three ways to represent integers in computer. They are as follows:

1. Sign Magnitude Representation (SMR)
2. 1’s Complement Representation
3. 2’s Complement Representation

1. SMR:
Normally a number has two parts sign and magnitude, eg: Consider a number +5. Here + is the sign and 5 is the magnitude. In SMR the most significant Bit (MSB) is used to represent the sign. If MSB is 0 sign is +ve and MSB is 1 sign is – ve.
eg: If a computer has word size is 1 byte then

Here MSB is used for sign then the remaining 7 bits are used to represent magnitude. So we can represent 27 = 128 numbers. But there are negative and positive numbers. So 128 + 128 = 256 number. The numbers are 0 to +127 and 0 to -127. Here zero is repeated. So we can represent 256 – 1 = 255 numbers.

2. 1 ‘s Complement Representation: To get the 1’s complement of a binary number, just replace every 0 with 1 and every 1 with 0. Negative numbers are represented using 1’s complement but +ve number has no 1’s complement.
eg: To find the 1’s complement of 21 +21 = 00010101
To get the 1 ‘s complement change all 0 to 1 and all 1 to 0.
-21 = 11101010
1’s complement of 21 is 11101010

3. 2’s Complement Representation: To get the 2’s complement of a binary number, just add 1 to its 1’s complement +ve number has no 2’s complement.
eg: To find the 2’s complement of 21 +21 =00010101
First take the 1’s complement for this change all 1 to 0 and all 0 to 1

2’s complement of 21 is 1110 1011

Question 13.
Write short notes about Unicode (3)
Answer:
It is like ASCII Code. By using ASCII, we can represent limited number of characters. But using Unicode we can represent all of the characters used in the written languages of the world.
eg: Malayalam, Hindi, Sanskrit .

Question 14.
Match the following.

1. (106)10	a. (171.53125)10
2. (71.24)8	b. (6a)16
3. (AB.88)16	c. (20)8
4. (10)16	d. (10000000)2
5. (128)10	e. (10)16
6. (16)10	f. (57.3125)10

Answer:
1 – b, 2 – f, 3 – a, 4 – c, 5 – d, 6 – e

Question 15.
Find the largest number in the list.

1. (1001)₂
2. (A)₁₆
3. (10)₈
4. (11)₁₀

Answer:
Convert all numbers into decimal
1. (1001)₂ = 1 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰
= 8 + 0 + 0 + 1
= (9)₁₀

2.) (A)₁₆ = (10)₁₀

3. (10)₈ = 1 × 8¹+0 × 8⁰
= (8)₁₀
So the largest number is 4 – (11)₁₀

Question 16.
Subtract 10101 from 1111 by using 2’s complement method.
Answer:
To subtract a number from another number find the 2’s complement of the subtrahend and add it with the minuend. Here subtrahend is 10101 and minuend is 1111 First take the 1’s complement of subtrahend and add 1 to it.
1’s complement of 10101 is 01010 add 1 to it

Here is no carry. So the result, is -ve and take the 2’s complement of 11010 and put a -ve symbol. So 1’s complement of 11010 is 00101 add 1 to this

So the result is -00110

Question 17.
Mr. Geo purchased (10)₂ kg sugar @Rs. (110 10)₂ and (1010)₂ kg Rice @Rs. (10100)₂. So how much rupees he has to pay in decimal.
Answer:
Convert each into decimal number system multiply and sum it up.
(10)₂ = (2)₁₀

(11010)₂ = 1 × 2⁴ + 1 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2¹
= 16 +8 + 0 +2 + 0
= (26)₁₀

(1010)₂ = 1 × 2³ + 0 × 2² + 1 × 2¹ +0 × 2⁰
= 8 + 0 + 2 + 0
= (10)₂

(10100)₂ = 1 × 2⁴ + 0 × 2³ + 1 × 2² +0 × 2¹ + 0 × 2⁰
= 16 + 0 + 4 + 0 + 0
= (20)₂
therfore 2 × 26 + 10 × 20
= 52 + 200
= 252
So Mr. Geo has to pay Rs. 252/-

Question 18.
Mr. Vimal purchased a pencil @ Rs. (101)2, a pen @ Rs. (1010)2 and a rubber @ Rs. (10)2. So how much rupees he has to pay in decimal.
Answer:
Add 101 + 1010 + 10

then convert (10001)₂ into decimal
(10001)₂ = 1 × 2⁴ + 0 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰
= 16 + 0 + 0 + 0 + 1
= (17)₁₀
So Mr. Vimal has to pay Rs. 17/-

Question 19.
Mr. Antony purchased 3 books worth Rs. a total of (1100100)₂. Atlast he returned a book worth Rs. (11001)₂. So how much amount he has to pay for the remaining two books in decimal number sys¬tem.
Answer:

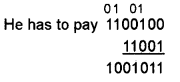
then convert (1001011 )₂ into decimal
(1001011)₂ = 1 × 2⁶ + 0 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 0 × 2² + 1 × 2¹ + 1 × 2⁰
=64 + 0 + 0 + 8 + 0 + 2 + 1
= (75)₁₀
So he has to pay Rs. 75/-

Question 20.
Mr. Leones brought two products from a super market a total of Rs. (11010010)₂ and he got a dicount of Rs. (1111)₂ So how much he has to pay for this products in decimal number system.
Answer:
Substract (1111)₂ from (11010010)₂

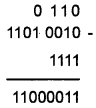
then convert (11000011)₂ into decimal
(11000011)₂ = 1 × 2⁷ + 1 × 2⁶ + 0 × 2⁵ + 0 × 2⁴ + 0 × 2³ + 0 × 2² + 1 × 2¹ + 1 × 2⁰
=128 + 64 + 0 + 0 + 0 + 0 + 2 + 1
= (195)₁₀

Question 21.
A textile showroom sells shirts with a discount of Rs. (110010)₂ on all barads. Mr. Raju wants to buy a shirt worth Rs. (11111000)₂. So after discount how much amount he has to pay in decimal.
Answer:
Substract (110010)₂ from (11 111 000)₂

then convert (11000110)₂ into decimal
(11000110)2 = 1 × 2⁷ + 1 × 2⁶ + 0 × 2⁵ + 0 × 2⁴ + 0 × 2³ + 1 × 2² + 1 × 2¹ + 0 × 2⁰
= 128 + 64 + 0 + 0 + 0 + 4 + 2 + 0
= (198)₁₀

Question 22.
Mr. Lijo purchased a product worth Rs. (1110011)₂ and he has to pay VAT @ Rs. (1100)₂. Then calculate the total amount he has to pay in decimal.
Answer:
Add (1110011)₂ and (1100)₂

then convert (1111111)₂ into decimal
(1111111)₂ = 1 × 2⁶ + 1 × 2⁵ + 1 × 2⁴ + 1 × 2³ + 1 × 2² + 1 × 2¹ + 1 × 2⁰
= 64 + 32 + 16 + 8 + 4 + 2 + 1
= (127)₁₀

Question 23.
By using truth table, prove the following laws of Boolean Algebra.

1. Idempotent law
2. Involution law

Answer:
1. A + A = A
A = A = A

2. (A¹)¹ = A

Question 24.
Consider the logical gate diagram.

1. Find the logical expression for the circuit given.
2. Find the compliment of the logical expression.
3. Draw the circuit diagram representing the compliment.

Answer:
1. \((x+\bar{y}) \cdot z\)

2. \((\bar{x} . y)+\bar{z}\)
3.

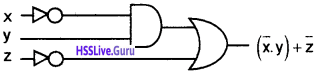
Question 25.
Draw the logic circuit diagram for the following Boolean expression.
\(A \cdot(\bar{B} + \bar{C})+\bar{A} \bar{B} \bar{C}\)
Answer:

Question 26.
Consider a bulb with three switches x, y and z. Write the Boolean expression representing the following states.

1. All the switches x, y and z are ON
2. x is ON and y is OFF or Z is OFF
3. Exactly one switch is ON.

Answer:

1. xy . z
2. \(x \bar{y}+\bar{z}\)
3. \(x . \bar{y} . \bar{z}+\bar{x} . y . \bar{z}+\bar{x} . \bar{y} . \bar{z}\)

Question 27.
Match the following.

A	B
i. Idem potent law	a. x + (y + z)=(x + y)+z
ii. Involution law	b. x + xy = x
iii. Complementarity law	c. x + y = y + x
iv. Commutative law	d. xx- 0
v. Absorption law	e. x = x
vi. Associative law	f. x + x = x

Answer:
i – f, ii – e, iii – d, iv – c, v – b, vi – a

Question 28.
Explain the principle of duality.
Answer:
It states that, starting with a Boolean relation, another Boolean relation can be derived by

1. Changing each OR sign (+) to a AND sign (.)
2. Changing each AND sign (.) to an OR sign (+)
3. Replacing each 0 by 1 and each 1 by 0.

The relation derived using the duality principle is called the dual of the original expression,
eg: x + 0 = x is the dual of x . 1 = x

Question 29.
Draw the circuit diagram for \(F=A \bar{B} C+\bar{C} B\) using NAND gate only.
Answer:
\(F=A \bar{B} C+\bar{C} B\)
= (A NAND (NOT B) NAND C) NAND ((NOT C) NAND B)

Question 30.
Draw a logic diagram for the function f = YZ + XZ using NAND gates only.
Answer:
f = YZ + XZ
= (Y NAND Z) NAND (X NAND Z)

Question 31.
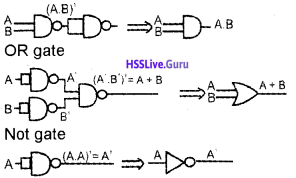
How do you make various basic logic gates using NAND gates.
Answer:
1. AND operation using NAND gate,
A.B = (A NAND B) NAND (A NAND B)

2. OR operation using NAND gate,
A + B = (A NAND A) NAND (B NAND B)

3. NOT operation using NAND gate,
NOT A = (A NAND A)

Question 32.
Which of the following Boolean expressions are correct? Write the correct forms of the incorrect ones.

1. A + A¹ = 1
2. A + 0 = A
3. A . 1 = A
4. A . A¹ = 1
5. A + A . B = A
6. A . (A + B) = A
7. A + 1=1
8. \((\overline{\mathrm{A} . \mathrm{B}})=\overline{\mathrm{A}} . \overline{\mathrm{B}}\)
9. A + A¹B = A + B
10. A + A = A
11. A + B . C = (A+B) . (B+C)

Answer:

1. Correct
2. Correct
3. Correct
4. Wrong, A . A¹ = 0
5. Correct
6. Correct
7. Correct
8. Wrong \(\overline{\mathrm{A} . \mathrm{B}}=\overline{\mathrm{A}}+\overline{\mathrm{B}}\)
9. Correct
10. Correct
11. Wrong, A + B . C = (A + B) . (A + C)

Question 33.
Prove algebraically that (x + y)’ . (x’ + y’) = x’ . y’
Answer:
LHS = (x + y)’ . (x’ + y’)
= (x’ . y’) . (x’ . y’)
= x’ . y’ . x’ + x’ . y’ . y’
= x’ . y’ + x’ . y’
= x ‘. y’ = RHS
Hence proved.

Question 34.
Give the complement of the following Boolean Expression.

1. (A + B) . (C + D)
2. (P + Q) + (Q + R) . (R + P)
3. (B + D’) . (A + C’)

Answer:
1. ((A+B) . (C+D))1 = (A+B)’ + (C+D)’
= A’ . B’ + C’ . D’

2. ((P+Q) + (Q+R) . (R.P))’ = (P+Q) ‘. ((Q+R) . (R+P))’
= P’ . Q’ . (Q+R)’ + (R+P)’
= P’ . Q’ . (Q’ . R’ + R’ . P’),

3. ((B+D’).(A+C’))’ = (B+D’)’0 + (A+C’)’
= B’ . D” + A’ . C”
= B’ . D + A’ . C

Question 35.
State and prove the idempotent law using truth table. Idempotent law
Answer;
Idempotent law states that

1. A + A = Aand
2. A . A = A Proof

1. A + A = A
Truth table is as follows:

ie. A + A = A as it is true for both values of A. Hence proved.

2. A . A = A
Truth table is as follows:

ie. A . A = A itself. It is true for both values of A. Hence proved.

Question 36.
State the Absorption laws of Boolean algebra with the help of truth tables.
Answer:
Absorption law states that
A + A . B = A and A . (A + B) = A
Proof:
The Truth table of the expression A + A . B=A is as follows.

Here both columns A and A + A . B are identical. Hence proved.
For A . (A + B) = A, the truth table is as follows:

Both columns A & A . (A + B) are identical. Hence proved

Question 37.
State Demorgen’s laws. Prove anyone with truth table method.
Answer:
Demorgan’s first theorem states that (A + B)’ = A’ . B’
ie. the complement of sum of two variables equals product of their complements,

The second theorem states that (A . B)’ = A’ + B’
ie. The complement of the product of two variables equals the sum of the complement of that variables.
Proof:
Truth table of first one is as follows:

From the truth table the columns of both (A + B)’ and A’ . B’ are identical. Hence proved.

Question 38.
Fill in the blanks:

1. (0.625)₁₀ = (……….)₂
2. (380)₁₀ = (……..)₁₆
3. (437)₈ = (………)₂

Answer:

1. (0.101)₂
2. (17C)₁₆
3. (100 011 111)₂

Question 39.
What do you mean by universal gates? Which gates are called Universal gates? Draw their symbols.

OR

Construct a logical circuit for the Boolean expression \(\bar{a} \cdot b+a \cdot \bar{b}\). Also write the truth table.
Answer:
Universal gates:
By using NAND and NOR gates only we can create other gate hence these gates are called Universal gate.
NAND gate:

NOR gate:

Truth table:

Logical circute:

Question 40.
Computers uses a fixed number of bits to respresent data which could be a number, a character, image, sound, video etc. Explain the various methods used to represent characters in memory.
Answer:
Representation of characters.
1. ASCII(American Standard Code for Information Interchange):
It is 7 bits code used to represent alphanumeric and some special characters in computer memory. It is introduced by the U.S. government. Each character in the keyboard has a unique number.
eg: ASCII code of ‘a’ is 97.

When you press ‘a’ in the keyboard , a signal equivalent to 1100001 (Binary equivalent of 97 is 1100001) is passed to the computer memory. 2⁷ = 128, hence we can represent only 128 characters by using ASCII. It is not enough to represent all the characters of a standard keyboard.

2. EBCDIC(Extended Binary Coded Decimal Interchange Code):
It is an 8 bit code introduced by IBM(International Business Machine). 2⁸ = 256 characters can be represented by using this.

3. ISCII(Indian Standard Code for Information Interchange):
It uses 8 bits to represent data and introduced by standardization committee and adopted by Bureau of Indian Standards(BIS).

4. Unicode:
The limitations to store more characters is solved by the introduction of Unicode. It uses 16 bits so 2¹⁶ = 65536 characters (i.e, world’s all written language characters) can store by using this.

Question 41.
Draw the logic circuit for the function
\(f(a, b, c)=a . b . c+\bar{a} . b+a . \bar{b}+a . b . \bar{c}\)

OR

Prove algebrically.
\(x . y+x . \bar{y} . z=x . y .+x . z\)
Answer:

OR

\(x \cdot y+x \cdot \bar{y} \cdot z=x \cdot(y+\bar{y} \cdot z)\)
= x . (y + z) = x . y + x . z
Hence proved.

Question 42.
Following are the numbers in various number systems. Two of the numbers are same. Identify them:

1. (310)₈
2. (1010010)₂
3. (C8)₁₆
4. (201)₁₀

OR

Consider the following Boolean expression:
(B’ + A)’ = B . A’
Identify the law behind the above expression and prove it using algebriac method.
Answer:
1. (310)₈ = 3 * 8² + 1 * 8¹ + 0 * 8⁰
= 192 + 8 + 0
= (200)₁₀

2. (1010010)₂ = 1 × 2⁶+ 0 × 2⁵ + 1 × 2⁴ + 0 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰
= 64 + 0 + 16 + 0 + 0 + 2 + 0
= (82)₁₀

3. (C8)₁₆ = C × 16 + 8 × 16⁰
= 12 × 16 + 8 × 1
= 192 + 8
= (200)₁₀
Here (a) (310)₈ and (C8)₁₆ are same

OR

This is De Morgan’s law (B’ + A’) = (B’)’ . A’
= B . A’
Hence it is proved

Question 43.
Find the decimal equivalent of hexadecimal number (2D)₁₆. Represent this decimal number in 2’s complement form using 8 bit word length.
Answer:
Convert (2D)₁₆ to binary number for this write down the 4 bit binary equivalent of each number

(2D)₁₆ = (00101101 )₂
First find the 1’s complement of (00101101 )₂ and add 1 to it

Hence 2’s complement is (11010011)₂

Question 44.
Answer any one question from 15(a) and 15(b).
1. Draw the logic circuit for the Boolean expression:
\((A+\overline{B C})+\overline{A B}\)

2. Using algebraic method prove that
\(\bar{Y} \cdot \bar{Z}+\bar{Y} \cdot Z+Y \cdot Z+Y=1\)
Answer:
1.

OR

2. L.H.S. = \(\bar{Y} \cdot \bar{Z}+\bar{Y} \cdot Z+Y Z+Y\)
= \(\bar{y} \cdot(\bar{z}+z)+y \cdot(z+1)\)
= \(\bar{y}. 1+\bar{y} \cdot 1=y \cdot y=1\)

Question 45.
With the help of a neat circuit diagram, prove that NAND gate is a universal gate.
Answer:
1. AND operation using NAND gate,
A . B = (A NAND B) NAND (A NAND B)

2. OR operation using NAND gate,
A + B = (A NAND A) NAND (B NAND B)

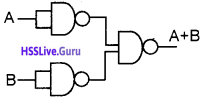
3. NOT operation using NAND gate,
NOT A = (A NAND A)

Question 46.
Boolean expression:
\((A+\overline{B C})+\overline{A B}\)

OR

Using algebraic method, prove that
\(\bar{Y} \cdot \bar{Z}+\bar{Y} \cdot Z+Y \cdot Z+Y=1\)
Answer:

OR

= Y . Z + Y . Z + Y . Z + Y
= Y . (Z + Z) + Y . (Z + 1)
= Y . 1 + Y. 1
= Y + Y
= 1
Hence the result.

Plus One Data Representation and Boolean Algebra Five Mark Questions and Answers

Question 1.
Explain the components of Data processing.
Answer:
Data processing consists of the techniques of sorting, relating, interpreting and computing items of data in orderto convert meaningful information. The components of data processing are given below.

1. Capturing data: In this step acquire or collect data from the user to input into the computer.
2. Input: It is the next step. In this step appropriate data is extracted and feed into the computer.
3. Storage: The data entered into the computer must be stored before starting the processing.
4. Processing/Manipulating data: It is a laborious work. It consists of various steps like computations, classification, comparison, summarization, etc. that converts input into output.
5. Output of information: In this stage we will get the results as information after processing the data.
6. Distribution of information: In this phase the information(result) will be given to the concerned persons/computers.

Question 2.
Define computer. What are the characteristics?
Answer:
A computer is an electronic device used to perform operations at very high speed and accuracy.
Following are the characteristics of the computer.

1. Speed: It can perform operations at a high speed.
2. Accuracy: It produces result at a high degree of accuracy.
3. Diligence: Unlike human beings, a computer is free from monotony, tiredness, lack of concentration etc. We know that it is an electronic ma chine. Hence it can work four hours without making any errors.
4. Versatility: It is capable of performing many tasks. It is useful in many fields.
5. Power of Remembering: A computer consists of huge amount of memory. So it can store and recall any amount of information. Unlike human beings, it can store huge amount of data and can be retrieved when needed.

Disadvantages of computer:

1. No. IQ: It has no intelligent quotient. Hence they are slaves and human beings are the masters. It can’t take its own decisions.
2. No feelings: Since they are machines they have no feelings and instincts. They can perform tasks based upon the instructions given by the humans (programmers)