Students can Download Chapter 3 Electrochemistry Notes, Plus Two Chemistry Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.
Kerala Plus Two Chemistry Notes Chapter 3 Electrochemistry
Electrochemistry-
branch of chemistry which deals with the inter-relationship between electrical energy and chemical changes.
Electrolysis – The chemical reaction occuring due to the passage of electric current (i.e., electrical energy is converted into chemical energy).
Electrochemical reaction –
The chemical reaction in which electric current is produced (i.e., chemical energy is converted into electrical energy). Example: Galvanic cell
Electrochemical Cell: – (Galvanic Cell/Voltaic Cell) :
It converts chemical energy into electrical energy during redox reaction, e.g. Daniell Cell
The cell reaction is
Zn(s) + Cu2+ (aq) Zn2+(aq) + Cu(s)
It has a potential equal to 1.1 V.

If an external opposite potential is applied in the Daniell ce|l, the following features are noted:
a) When Eext < 1.1 V,
(i) electrons flow from Zn rod to Cu rod and hence current flows from Cu rod to Zn rod.
(ii) Zn dissolves at anode and Cu deposits at cathode.
b) When Eext= 1.1 V,
(i) No flow of electrons or current,
(ii) No chemical reaction.
c) When Eext > 1.1 V
(i) Electrons flow from Cu to Zn and current flows from Zn to Cu.
(ii) Zn is deposited at the Zn electrode and Cu dissolves at Cu electrode.
![]()
Galvanic Cells :
In this device, the Gibbs energy of the spontaneous redox reaction is converted into electrical work.
The cell reaction in Daniell cell is a combination of the following two half reactions:
- Zn(s) → Zn2+(aq) + 2 \(\overline { e } \) (oxidation half reaction/ anode reaction)
- Cu2+(aq) + 2 \(\overline { e } \) → Cu(s) (reduction half-reaction/ cathode reaction)
These reactions occur in two different vessels of the Daniell cell. The oxidation half reaction takes place at Zn electrode and reduction half reaction takes place at Cu electrode. The two vessels are called half cells or redox couple. Zn electrode is called oxidation half cell and Cu electrode is called reduction half cell. The two half-cells are connected externally by a metallic wire through a voltmeter and switch. The electrolyte of the two half-cells are connected internally through a salt bridge.
Salt Bridge :
It is a U-shaped glass tube filled with agar-agar filled with inert electrolytes like KCl, KNO3, NH4NO3.
Functions of Salt Bridge :
- It maintains the electrical neutrality of the solution by intermigration of ions into two half-cells.
- It reduces the liquid-junction potential.
- It permits electrical contact between the electrode solutions but prevents them from mixing.
Electrode potential –
potential difference developed between the electrode and the electrolyte. According to IUPAC convention, the reduction potential alone is called electrode potential and is represented as \(E_{M^{n+} / M}\)
Standard Electrode Potential :
The electrode potential understandard conditions, (i.e., at 298 K, 1 atm pressure and 1M concentrated solution) is called standard electrode potential. It is represented as EΘ.
Representation of a Galvanic Cell :
A galvanic cell is generally represented by putting a vertical line between metal and electrolyte solution and putting a double vertical line between the two electrolytes connected by a salt bridge.
For example, the Galvanic cell can be represented as,
Zn (s)|Zn2+(aq)||Cu2+(aq)|Cu(s)
Cell Potential or EMF of a Cell :
The potential difference between the two electrodes of a galvanic cell is called cell potential (EMF) and is measured in volts.
EMF = Ecell = Ecathode – Eanode = ERjght – ELeft
Consider a cell, Cu(s) | Cu22+ (aq) || Ag+ (aq) | Ag(s)
Ecell = Ecathode – Eanode = EAg+/Ag – ECu2+/Cu
How to calculate emf of a cell when concentration varies from standard conditions.
Measurement of Electrode Potential using Standard Hydrogen Electrode (SHE)/Normal Hydrogen Electrode :
SHE or NHE consists of a platinum electrode coated with platinum black. The electrode is dipped in an exactly 1 M HCl solution and pure H2 gas at 1 bar is bubbled through it at 298 K. The electrode potential is arbitrarily fixed as zero at all temperatures.

Representation of SHE/NHE :
When SHE acts as anode:
Pt(s), Hsub>2(g, 1 bar) / H+(aq, 1 M)
When SHE acts as cathode:
H+(aq, 1 M)/H2(g, 1 bar), Pt(s)
![]()
Electrochemical Series/Activity series :
The arrangement of various elements in the increasing or decreasing order of their standard electrode potentials.
Applications of Electrochemical Series:
1. To calculate the emf of an electrochemical cell – The electrode with higher electrode potential is taken as cathode and the other as anode.
\(E_{\mathrm{cell}}^{\Theta}=E_{\mathrm{cathode}}^{\Theta}-E_{\mathrm{anodo}}^{\Theta}\)
2. To compare the reactivity of elements – Any metal having lower reduction potential (electode potential) can displace the metal having higher reduction potential from the solutions of their salt, e.g. Zn can displace Cu from solution.
Zn(s) + CuSO4(aq) → ZnSO4(aq) + Cu(s)
3. To predict the feasibility of cell reactions -If EMF is positive, the cell reaction is feasible and if it is negative the cell reaction is not feasible.
4. To predict whether H2 gas will be evolved by reaction of metal with acids – All the metals which have lower reduction potentials compared to that of H2 electrode can liberate H2 gas from acids.
5. To predict the products of electrolysis.
Nernst Equation :
It gives a relationship between electrode potential and ionic concentration of the electrolyte. For the electrode reaction,
Mn+ (aq) + n \(\overline { e } \) → M(s)
the electrode potential at any concentration measured with respect to SHE can be represented by,

R = gas constant (8.314 J K-1 mol-1), T=temperaturein kelvin, n = number of electrons taking part in the electrode reaction, F = Faraday constant (96487 C mol-1)
By converting the natural logarithm to the base 10 and subsitituting the values of R(8.314 J K-1 mol-1),T (298 K) and F (96487 C mol-1) we get,
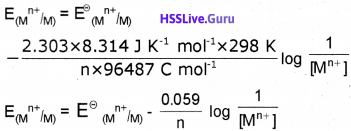
Nernst Equation for a Galvanic Cell :
In Daniell cell, the electrode potential for any concentration of Cu2+ and Zn2+ ions can be written as,

Converting to natural logarithm to the base 10 and substituting the values of R, F and T=298 K, it. reduces to
![]()
Consider a general electrochemical reaction,

Equilibrium Constant and Nernst Equation:

where Kc is the equilibrium constant.
Electrochemical Cell and Gibbs Energy of the Reaction (∆rG):

Conductance of Electrolytic Solutions: .Conductors:
A substance which allows the passage of electricity through it. Conductor are classified as,
Metallic or Electronic Conductors:
In these the conductance is due to the movement of electrons and it depends on:
- The nature and structure of the metal
- Number of valence electrons per atom
- Temperature (it decreases with increase in temperature)
e.g. Ag, Cu, Al etc.
ii. Electrolytic Conductors
Electrolytes – The substances which conduct electricity either in molten state or in solution, e.g. NaCl, NaOH, HCl, H2SO4 etc. The conductance is due to the movement of ions. This is also known as ionic conductance and it depends on:
- Nature of the electrolyte
- Size of the ions and their solvation
- Nature of the solvent and its viscosity
- Concentration of the electrolyte
- Temperature (it increases with increase in temperature)
Ohm’s law – It states that the current passing through a conductor (I) is directly proportional to the potential difference (V) applied.
i.e., I ∝ V or I = \(\frac{V}{R}\)
where R – resistance of the conductor- unit ohm. In SI base units it is equal to kg m²/s³ A²
![]()
The electrical resistance of any substance/object is directly proportional to its length T, and inversly proportional to its area of cross section ‘A’.
R ∝ \(\frac{\ell}{\mathrm{A}}\) or R = ρ\(\frac{\ell}{\mathrm{A}}\) where,
ρ – (Greek, rho) – resistivity/specific resistance – SI unit ohm metre (Ω m) or ohm cm (Ω cm).
Conductance (G):
inverse or reciprocal of resistance (R).
\(G=\frac{1}{R}=\frac{A}{\rho \ell}=\kappa \frac{A}{\ell}\)
where K = \(\frac{1}{\rho}\) called conductivity or specific conductance (K – Greek, kappa)
SI unit of conductance – S (siemens) or ohm-1.
SI unit of conductivity – S m-1
1 S cm-1 = 100 S m-1
Molar Conductance of a Solution (Λm):
It is the conductance of the solution containing one mole of the electrolyte when placed between two parallel electrodes 1 cm apart. It is the product of specific conductance (K) and volume (V) in cm³ of the solution containing one mole of the electrolyte.
![]()
where M is molarity of the solution.
Unit of Λm is ohm’1 cm2 mol’1 Or S cm² mol-1
Λm = \(\frac{K}{C}\) [C-Concentration of the solution.]
Measurement of the Conductivity of Ionic Solutions :
The measurement of an unknown resistance can be done by Wheatstone bridge. To measure resitance of the electrolyte it is taken in a conductivity cell. The resistance of the conductivity cell is given by the equation.
\(R=\rho \frac{\ell}{A}=\frac{1}{\kappa A}\)

The quantity \(\frac{\ell}{\mathrm{A}}\) is called cell constant and isdenoted A by G*. It depends on the distance (/) between the electrodes and their area of cross-section (A).
Variation of Conductivity and Molar Conductivity with Concentration :
Conductivity (K) always decreases with decrease in concentration both for weak and strong electrolytes. This is because the number of ions per unit volume that carry the current in a solution decreases on dilution.
Molar conductivity (Λm) increases with decrease in concentration. This is because the total volume, V of the solution containing one mole of electrolyte also increases.
The variation of molar conductance is different for strong and weak electrolytes,
1. Variation of Λm with Concentration for Strong Electrolytes:
The molar conductance increases slowly with decrease in concentration (or increase in dilution) as shown below:

There is a tendency for Λm to approach a certain limiting value when concentration approaches zero i. e., dilution is infinite. The molar conductance of an electrolyte when the concentration approaches zero is called molar conductance at infinite dilution, Λm∞ or Λ°m. The molar conductance of strong electrolytes obeys the relationship.
Λm = Λ°m -AC1/2 where C = Molar concentration, A = constant for a particular type of electrolyte.
This equation is known as Debye-Huckel-Onsagar equation.
2. Variation of Λm with Concentration for Weak Electrolytes :
For weak electrolytes the change in Λm with dilution is due to increase in the degree of dissociation and consequently increase in the number of ions in total volume of solution that contains 1 mol of electrolyte. Here, Λm increases steeply on dilution, especially near lower concentrations.

Thus, the variation of Λm with √c is very large so that we cannot obtain molar conductance at infinite dilution Λ°m by the extrapolation of the graph.
Kohlrausch’s Law:
The law states that, the molar conductivity of an electrolyte at infinite dilution is equal to the sum of the molar ionic conductivities of the cations and anions at infinite dilution.
Λ°m = γ+ λ°+ + γ– λ°–
λ°+ and λ°– are the molar conductivities of cations and anions respectively at infinite dilution, Y+ and V. are number of cations and anions from a formula unit of the electrolyte.
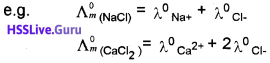
Applications of Kohlaransch’s Law
1) To calculate Λ°m of weak electrolytes
2) To calculate degree of dissociation of weak electrolytes
\(\alpha=\frac{\Lambda_{m}}{\Lambda_{m}^{0}}\)
3) To determine the dissociation constant of weak electrolytes

Electrolytic Cell and Electrolysis:
In an electrolytic cell, external source of voltage is used to bring about a chemical reaction. Electrolysis is the phenomenon of chemical decomposition of the electrolyte caused by the passage of electricity through its molten or dissolved state from an external source.
![]()
Quantitative Aspects of Electrolysis
Faraday’s Laws of Electrolysis First Law:
The amount of any substance liberated or deposited at an electrode is directly proportional to the quantity of electricity passing through the
electrolyte.
w α Q where ‘Q’ is the quantity of electric charge in coulombs.
w = ZQ .
w = Zlt
(∵ Q = It) where T is the current in amperes , ‘t’ is the time in seconds and ‘Z’ is a constant called electrochemical equivalent.
Second Law:
The amounts of different substances liberated by the same quantity of electricity passing through the electrolytic solution are proportional to their chemical equivalent weights.
![]()
The quantity of electricity required to liberate/deposit 1 gram equivalent of any substance is called Faraday constant ‘F’.
1 F = 96487 C/mol ≈ 96500 C/mol
Products of Electrolysis:
It depend on the nature of the material being electrolysed and the type of electrodes being used.
Electrolysis of Sodium Chloride:
When electricity is passed through molten NaCl, Na is deposited at the cathode and Cl2 is liberated at the anode.
Na+(aq) + \(\overline { e } \) → Na(s) (Reduction at cathode)
Cl–(aq) → ½ Cl2(g) + \(\overline { e } \) (Oxidation at anode)
When concentrated aqueous solution of NaCl is electrolysed, Cl2 is liberated at anode, but at cathode H2 is liberated instead of Na deposition due to the high reduction potential of hydrogen.
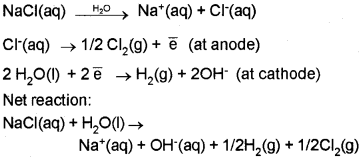
The resultant solution is alkaline due to the formation of NaOH.
Electrolysis of CuSO4 :
When aqueous CuSO4 solution is electrolysed using Pt electrodes, Cu is deposited at the cathode and O2 is liberated at the anode.
Cu2+(aq) + 2 \(\overline { e } \) → Cu(s) (at cathode)
H2O(l) → 2H+(aq) + 1/2 O2(g) + 2 \(\overline { e } \) (at anode)
If Cu electrode is used, Cu is deposited at cathode and an equivalent amount of Cu dissolves in solution from the anode (because oxidation potential of Cu is higherthan that of water).
Cu2+(aq) + 2 \(\overline { e } \) → Cu(s) (at cathode)
Cu(s) → Cu2+(aq) + 2\(\overline { e } \) (atanode)
Commercial Cells (Batteries)
The electrochemical cells can be used to generate electricity. They are two types:
i) Primary Cells:
Cells in which the electrode reactions cannot be reversed by external energy. These cells cannot be recharged, e.g. Dry cell, Mercury cell.
ii) Secondary Cells :
Cells which can be recharged by passing current through them in the opposite direction so that they can be used again.
e.g. Lead storage battery, Nickel-Cadmium cell.
Primary Cells
a) Dry Cell:
Anode – Zn container
Cathode – Carbon (graphite) rod surrounded by powdered MnO2 and carbon.
Electrolyte – moist paste of NH4Cl and ZnCl2
The electrode reactions are :
Anode : Zn → Zn2+ + 2 \(\overline { e } \)
Cathode: MnO2 + NH4+ + \(\overline { e } \) → MnO(OH) + NH3
Dry cell has a potential of nearly 1.5 V.
![]()
b) Mercury Cell:
Anode – Zn amalgam (Zn/Hg)
Cathode – paste of HgO and carbon
Eelectrolyte – paste of KOH and ZnO. The electrode reactions are,
Anode : Zn/Hg + 2OH– → ZnO(s) + H2O + 2 \(\overline { e } \)
Cathode : HgO + H2O + 2 \(\overline { e } \) → Hg(l) + 2 OH–
Overall reaction : Zn/Hg + HgO(s) → ZnO(s)+ Hg(l)
The cell potential = 1.35 V
2. Secondary Cells
a) Lead Storage Battery :
Anode – lead plates
Cathode – grids of lead plates packed with lead dioxide (PbO2)
Electrolyte – 38% (by weight) soution of H2SO4.
The cell reactions when the battery is in use are,
Anode: Pb(s) + SO42-(aq) → PbSO4 + 2 \(\overline { e } \)
Cathode: PbO2(s) + SO42-(aq) + 4H+(aq) + 2 \(\overline { e } \) → PbSO4(s) + 2H2O(I)
The overall cell reaction is,
Pb(s) + PbO2(s) + 2H2SO4(aq) → 2PbSO4(s) + 2H2O(l)
The emf of the cell depends on the concentration of H2SO4. On recharging the battery the reaction is reversed and PbSO4(s) on anode is converted to Pb and PbSO4(s) at cathode is converted into PbO2.
b) Nickel-Cadmium Cell:
Anode- Cd
Cathode – metal grid containing nickel (IV) oxide. Electrolyte – KOH solution. The overall cell reaction during discharge is,
Cd(s) +2 Ni(OH)3(s) → CdO(s) + 2Ni(OH)2(s) + H2O(l)
3) Fuel Cells :
These are Galvanic cells designed to convert the energy of combustion of fuels directly into electrical energy.
H2 – O2 fuel cell – In this, hydrogen and oxygen are bubbled through porous carbon electrodes into concentrated aqueous NaOH solution, which acts as the electrolyte.

The electrode reactions are,
Anode : 2H2(g) + 4OH–(aq) → 4H2O(l) + 4\(\overline { e } \)
Cathode : O2(g) + 2H2O(l) + 4\(\overline { e } \) → 4OH–(aq)
Overall reaction : 2H2(g) + O2(g) → 2H2O(l)
Advantages of Fuel Cells –
pollution free, more efficient than conventional methods, Runs continuously as long as the reactants are supplied, electrodes are not affected.
![]()
Other examples:
CH4 – O2 fuel cell, CH3OH – O2 fuel cell
Corrosion :
Any process of destruction and consequent loss of a solid metallic material by reaction with moisture and other gases present in the atmosphere. More reactive metals are corroded more easily. Corrosion is enhanced by the presence of impurities, air & moisture, electrolytes and defects in metals.
Examples: Rusting of iron, tarnishing of Ag.
Mechanism:
In corrosion a metal is oxidised by loss of electrons to O2 and form oxides. It is essentially an electro chemical phenomenon. At a particular spot of an object made of iron, oxidation take place and that spot behaves as anode.
2 Fe(s) → 2 Fe2+ + 4\(\overline { e } \)E° = -0.44 V
Electrons released at anodic spot move through metal and go to another spot on the metal and reduce 02 in presence of H+. This spot behaves as cathode.
O2(g) + 4 H+(aq) + 4\(\overline { e } \) → 2 H2O(l) E° = 1.23 V
The overall reaction is,
2 Fe(s) + O2(g)+ 4H+(aq) → 2 Fe2+ + 2H2O(I) E° = 1,67V
The ferrous ions are further oxidised by atmospheric 02 to ferric ions and form hydrated ferric oxide (rust) Fe2O3.xH2O
Prevention of Corrosion
1) Barrier Protection:
Coating the surface with paints, grease, metals like Ni, Cr, Cu etc.
2) Sacrificial Protection:
Coating the surface of iron with a layer of more active metals like Zn, Mg, Al etc. The process of coating a thin film of Zn on iron is known as galvanisation.
3) Anti-rust Solutions:
Applying alkaline phosphate/ alkaline chromate on iron objects which provide a protectve insoluble film. Also, the alkaline nature of the solutions decreases the availability of H+ ions and thus decreases the rate of corrosion.