You can Download Motion Questions and Answers, Summary, Activity, Notes, Kerala Syllabus 8th Standard Basic Science Solutions Chapter 9 help you to revise complete Syllabus and score more marks in your examinations.
Kerala State Syllabus 8th Standard Basic Science Solutions Chapter 9 Motion
We can state whether an object is in a state of rest or motion only with reference to another object. The object which is taken as reference is the reference body. Reference body is the object with respect to which the state of rest or motion of an object is described.
Distance and Displacement
If an object travels from initial position to final position through different routes the distance will not be equal. But if it travels through straight line the distance is called displacement. The distance has only magnitude. But displacement has both magnitude and direction.
While stating the displacement, it is necessary to indicate the direction along with the magnitude of the distance travelled. Such physical quantities having both magnitude and direction are referred to as vector quantities. Physical quantities of which the direction is not to be indicated, are scalar quantities When a body travels along a straight line in the same direction, the magnitude of its distance and displacement will be equal.
Kerala Syllabus 8th Standard Physics Notes Speed and Velocity
Speed is the distance travelled in unit time. Velocity is the displacement in unit time.

The unit of speed and velocity is metre/second (m/s)
Uniform speed and Non uniform speed
If a body in motion covers equal distance in equal intervals of time the body is said to have uniform speed. That is if a car travels 20 km in first 2 seconds, again travel 20 km in successive 2 seconds, the body is said to have uniform speed. But the body travels 20 km in first 2 seconds, 40 km in next 2 seconds and then travels 50 km in next 2 seconds the body is said to have non uniform speed.
The speed of a car in non uniform speed is different. So to find out the speed calculate the average speed

Uniform velocity and Non uniform velocity
A body has uniform velocity if it covers equal displacements in the same direction in equal intervals of time. But if it is not in equal velocity in equal interval it is in non uniform velocity.
Hss Live Guru 8th Physics Kerala Syllabus Acceleration
A body with a velocity of o m/s takes 5 seconds to rise the velocity to 5 m/s the change of velocity is 5 – o = 5 m/ s. The change is taken place in 5 sec. \(\frac{change of velocity}{time}\) the rate of change of velocity which is called acceleration.
Class 8 Physics Notes Kerala Syllabus Retardation
When the velocity of a body is decreasing the acceleration is negative. This type of acceleration is called retardation.
Carelessness of pedestrians is also one of the reasons for road accidents.
To reduce the accidents following precuations are to be taken.
- walk along the footpath only
- walk only along the right side of the road
- cross roads only at the zebra crossing.
- while walking along the road late in the evening or night avoid wearing black or dark coloured clothes.
- ATUL Pivot Point Calculator
Motion Textbook Questions and Answers
Kerala Syllabus 8th Standard Biology Notes Question 1.
Which of the following does not belong to the group?
(velocity, acceleration, speed, displacement)
Answer:
speed
Hsslive Guru 8th Class Physics Kerala Syllabus Question 2.
The statement of a child is as follows: “My displacement is zero though I ran 250 m”. What is meant by this?
Answer:
The child reaches the point which he started. So the displacement is o.
Class 8 Physics Kerala Syllabus Question 3.
All objects having uniform speed need not have uniform velocity. Describe with the help of examples.
Answer:
If a body is in uniform velocity the direction and quantity will be equal.

In figure (1) from A to B and B to C the direction is different. Therefore it is not in uniform velocity. In figure (2) it is in uniform velocity.
Kerala Syllabus 8th Standard Physics Question 4.
Bus A covered 75 m in 5 s. Bus B covered 169 m in 13 s
a. Which bus covered a greater distance?
b. Which bus has a higher speed?
Answer:
The bus B covered more distance.
b. Speed = \(\frac{distance}{time}\)
Speed of A= \(\frac{75}{5}\) = 15 m/s
Speed of B = \(\frac{169}{13}\) = 13 m/s
So the bus A has higher speed
Kerala Syllabus 8th Standard Physics Notes Pdf Question 5.
What is the acceleration of a car which started from rest and acquired a velocity of 40 m/s in 8 s?
Answer:

Physics Notes Class 8 Kerala Syllabus Question 6.
A car covered the first 400 m distance with a speed of 8 m/s, the next 1200 111 with a speed 12 m/s and the last 360 m with a speed of 12 m/s. Calculate the average speed of the car.
Answer:
Average speed = \(\frac{Total distance travelled}{time taken to trvel the distance}\)
Time taken to travel the distance 400m = \(\frac{400}{8}\) = 50s
Time taken to travel the distance 1200m = \(\frac{1200}{10}\) = 120s
Time taken to travel the distance 360m = \(\frac{360}{12}\) = 30s
Total distance travelled = 400 + 1200 + 360 = 1960m
Total time to travel = 50 + 120 + 30 = 200s
Average speed=\(\frac{1960}{200}\)= 9.8 m/s
Physics Notes For Class 8 Kerala Syllabus Question 7.
Does a body have acceleration in the following situations? Why?
- body travelling along a straight line with uniform velocity.
- body travelling along a straight line with non-uniform velocity.
- body travelling along a circular path with uniform speed.
- body travelling along a circular path with non-uniform speed.
Answer:
- body travelling along a straight line with non-uniform velocity.
- body travelling along a circular path with non-uniform speed.
If an object should have acceleration it should be travelled in non uniform speed or in non uniform velocity.
Change in velocity time
Acceleration = \(\frac{change in velocity}{time}\)
Basic Science Class 8 Chapter 9 Kerala Syllabus Question 8.
A lorry travelling with a velocity of 30 m/s came to rest in 5 s. What is its acceleration?
Answer:
Acceleration = \(\frac{0 – 30}{5}\) = 6m/s²
∴ Retardation = 6m/s²
Hsslive Guru 8th Basic Science Kerala Syllabus Question 9.
What is the displacement of a car in 30 s if it is travelling with a velocity of 15 m/s?
Answer:
Velocity = \(\frac{dispalcement}{time}\)
Displacement = velocity × time = 15 × 30 = 450m
Hss Live Guru 8th Basic Science Kerala Syllabus Question 10.
Observe the figure showing the path of a body which started from
A and moved to C through B.

a. Calculate the speed of the body.
b. What is the velocity of the body?
c. What is the velocity of the body if it has taken 5 s to reach A hack from C?
d. Compare the velocity of the body when it reached C from A and also when it reached A from C.
Answer:
a. Distance = 60 + 40 = 100 m
Time = 6 + 4 = 10 sec
∴ Speed = \(\frac{100}{10}\) = 10m/s
b. Velocity = \(\frac{dispalcement}{time}\) = \(\frac{70}{10}\) = 7m/s
c. displacement = 0, Velocity = 0
d. Velocity of the body when it reached C from A = 7 m/s
Velocity of the boby when it reached A from C velocity = 0 m/s
Motion Additional Questions and Answers
Hsslive Guru Physics 8th Standard Kerala Syllabus Question 1.
Observe the figure in which a child travelled from A to B and returned from B to A.

a. Are the distance from A to B and B to A through C be equal?
b. What is the difference between the distance between A to B and return to B through C?
c. Which is the displacement ?
Answer:
a. No
b. The path from A to B is straight path. But the path from B to A is curved.
c. A to B
Basic Science For Class 8 Chapter 9 Kerala Syllabus Question 2.
If a stone is thrown up 8 m perpendicularly and it falls in hand itself,
a. What is the distance travelled by the stone when it is thrown up and what is the displacement?
b. What is the distance when it fell in hand and what is the displacement?
Answer:
a. Distance = 8m, displacement = 8m
b. Distance = 16m, displacements = 0
Basic Science Class 8 Chapter 9 Solutions Kerala Syllabus Question 3.

A man start from A travelled through B, C and D reaches at A. Complete the table below.

Answer:

Basic Science Class 8 Pdf Notes Kerala Syllabus Question 4.
Tabulate the difference between distance and displacement
Answer:
| Distance | displacement |
| Scalar quantity | Vector quantity |
| Motion in different direction | Straight line motion |
Question 5.
A car travels a distance of 15m from A to B in 2 s, a distance of 25 m from B to C in 3 s, a distance of 8 m from C to D in 1 s.
a. What is the total distance travelled?
b. What is the total time taken to travel this distance?
c. What is the average speed of the car?
Answer:
a. 48 m
b. 6 Sec
![]()
Question 6.
Write examples of uniform velocity and non uniform velocity.
Answer:
mniform velocity : Travelling 9# light non uniform velocity : Travelling of bus
Question 7.
What is the acceleration when a car started from rest raised a velocity 80 m/s in 10 s?
Answer:
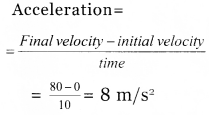
Question 8.
Complete the table using the figure below.

Answer:
Travelled position acceleration

Question 9.
Write 3 occasions of occurrence of acceleration.
Answer:
1. Falling of coconut from coconut tree.
2. Rolling of wheel on a slope.
3. A train starting from the station.
Question 10.
write three methods to reduce road accidents.
Answer:
1. walk along the footpath only
2. Avoid over speed, Avoid drink and drive
Question 11.
Brakes are applied suddenly to a racing car travelling at 50m/s. If the car stops after 20 seconds, calculate the retardation of the car.
Answer:
Initial velocity of the car (u) = 50 m/s
Final velocity of the car (v) = o (The car stops)
Time = 20s
![]()
When it is written as retardation, no negative sign is required.
∴ Retardation of the car = 2.5 m/s²
Question 12.
Classify the following quantities into Scalar and Vector quantities.
Distance, Displacement, Time, Speed, Velocity, Acceleration.
Answer:
| Scalar | Vector |
| Distance | Displacement |
| Time | Velocity |
| Speed | Acceleration |
Question 13.
Velocity is a vector quantity. What do you mean by vector quantities? Write examples.
Answer:
Quantities having both magnitude and direction are called vector quatities. eg: Displacement, Acceleration.
Question 14.
Compare distance and displacement.
Answer:
The length of the path covered by a body is known as distance. This is a scalar quantity. This is measured in a standard unit metre. The straight line distance between initial and final positions of a moving body is called displacement. This is a vector quantity. This is measured in metre.
Question 15.
A cheetah can start from rest and attain the velocity 72 km/h in 2 seconds. Calculate the acceleration of cheetah.
Answer:

Question 16.
Given figure shows the two ways in which a person reached at C
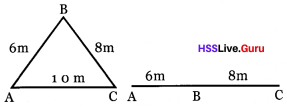
Reach at C from A through B ,
then
a. From fig.1 what is the total di-stance travelled? What is the total displacement covered?
b. From fig.2 what is the total distance travelled by the person? What is the total displacement covered by him?
c. find out the situation in which distance and displacement are equal by comparing given measures?
Answer:
a. Distance = 14 m
Displacement = 10 m
b. Distance = 14 m,
Displacement = 14 m
c. Only when a moving object travelling in a straight line on same direction.













