Students can Download Chapter 13 Nuclei Notes, Plus Two Physics Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.
Kerala Plus Two Physics Notes Chapter 13 Nuclei
Introduction
In this chapter, We shall discuss various properties of nuclei such as their size, mass and stability, and also associated nuclear phenomena such as radioactivity, fission and fusion.
Atomic Masses And Composition Of Nucleus
1. Atomic Mass Unit (amu or u):
The most commonly used unit to express atomic mass of nucleus is atomic mass unit (u). It is defined as 1/12th of mass of carbon atom (C12).

![]()
2. Proton:
The nucleus of lightest atom (isotope) of hydrogen is called proton. The mass of proton is
mp = 1.00727u = 1.67262 × 10-27 kg
The charge of proton is +1.6 × 10-19 and it is stable.
3. Discovery of Neutron:
Neutron was discovered by James Chadwick. He bombarded Beryllium nuclei with α particles and observed the emission of neutral radiation. He assumed the neutral radiation consists of neutral particles called neutron.
4. Neutron:
Neutron is changeless particle of mass 1.6749 × 10-27kg. Neutron is stable inside nucleus but it is unstable in its free state.
5. Representation of Nuclide:
Nuclear species or nuclides are represented by notation AZX, where X is the chemical symbol of species.
Z → Atomic Number = Number of protons (electrons)
N → Neutron Number = Number of neutrons
A → Mass Number = Z + N (Total number of protons and neutrons)
6. Isotopes, Isobars and Isotones:

Size Of The Nucleus
The radius of nucleus is related to mass number (A) by the equation
R = R0A1/3
where 0 = 1.2 × 10-15 m
The volume of nucleus (the shape of nucleus is assumed to be spherical) is proportional to A.
ie. Volume = \(\frac{4}{3}\)πR3 = \(\frac{4}{3}\)R03.A
∴ Volume α A
The density of nucleus is constant. It is independent of A and its value is 2.3 × 1017kgm-3
![]()
Mass Energy And Nuclear Binding Energy
1. Mass Energy:
According to Einstein mass is considered as a source of energy. The mass ‘m’ can be converted into energy according to relation
E = mc2
This is mass energy equivalence relation. C is the velocity of light (3 × 108m/s).
2. Nuclear binding energy:
(A) Mass Defect:
The mass defect (Am) is the difference in the mass of nucleus and total mass of constituent nucleons.
∆m = (ZMP + (A – Z)mn] – M
mP and mn are mass of proton and neutron respectively. M is the mass of nucleus.
Eg: In 168O, there are 8 protons and 8 neutrons. The atomic mass of 118O is 15.99493u. The expected mass of 168O is sum of masses of its nucleons.
Total mass of nucleons
= 8 × mP + 8 × mn
= 8 × 1.00727u + 8 × 1.00866u
= 16.12744u
The difference in mass,
∆m = 16.12744u – 15.99493u = 0.13691u
(B) Binding Energy and Binding Energy per nucleon (Eb and Ebn):
Binding Energy: Mass defect (∆m) gets converted into energy as
Eb = ∆mc2
This energy is called binding energy. Which binds nucleons inside the nucleus.
Binding Energy per nucleon:
Binding energy per nucleon Ebn is the ratio of binding energy of nucleus to number of nucleons
Ebn = \(\frac{E_{b}}{A}\)
Ebn is the measure of stability of nucleus.
![]()
(C) Plot of Ebn versus mass number, A Main features of the graph:
- Ebn is almost constant for nuclei whose mass number ranges as 30 < A < 170. The maximum value of Ebn is 8.75Mev for 56Fe and it is 7.6MeV for 238U.
- Ebn is low for lighter nuclei and also for heavier nuclei.
- There appear narrow spikes in the curve.
The conclusions from the features of graph:
- The force is attractive and sufficiently strong.
- The nuclear force is short range. Each nucleon has its influence on its immediate neighbors only so nuclear force is saturated.
- Heavier nuclei like U238 have low Ebn. So it split up into nuclei of high Ebn releasing energy ie. it undergoes fission.
- Lighter nuclei like 2H, 3H, etc. have low Ebn. So it combine to form a heavier nuclei of high Ebn releasing energy ie. it undergoes nuclear fusion.
- The nuclei at the peaks of narrow spikes have high Ebn which shows extra stability.
Nuclear Force
The features of nuclear force are:
- The nuclear force is the strongest force in nature.
- The nuclear force is saturated. It is short range force.
- The nuclear force is charge independent ie. nuclear force between proton-proton, neutron-neutron, and proton-neutron are the same.
Variation of potential energy with distance:
The potential energy of a pair of nucleons as a function of their separation is shown in the figure
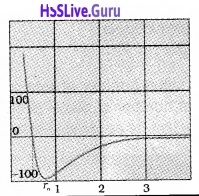

At a particular distance r0, potential energy is minimum. The force is attractive when r > r0 and it is repulsive when r < r0. The value of r0 is about 0.8fm.
![]()
Radioactivity
A.H. Becquerel discovered radioactivity.
In radioactive decay, unstable nucleus undergoes decay into stable one. There are three types of decay
- α decay
- β decay
- γ decay
1. Law of Radioactive Decay:
According to Law of Radioactive decay, the number of nuclei undergoing decay per unit time (or rate of decay) is proportional to number of nuclei in the sample at that time.

λ is decay constant or disintegration constant. The negative sign indicates that number of nuclei is decreasing with time. The solution to the above differential equation is
N = N0e-λt
N0 is the initial number of atoms. This equation shows that number of nuclei is decreasing exponentially with time as shown below.

Derivation of equation N(t) = N(0)e-λt
According to Law of Radioactive decay,
\(\frac{d N}{d t}\) = -λn
\(\frac{d N}{d t}\) = -λdt
Integrating
InN = -λt + C_____(1)
C is the constant of integration. To get value of C, let us assume that initially (t = 0) the number of nuclei be N0
∴ C = In N0
Substituting for C in equation (1) we get,
InN – In N0 = -λt
In\(\frac{N}{N_{0}}\) = -λt
\(\frac{N}{N_{0}}\) = e-λt
N = N0e-λt
![]()
(A) The decay rate (R):
The decay rate is number of nuclei disintegrating per unit time and is denoted by R.
R = \(\frac{-d N}{d t}\)
Differentiating the equation N = N0e-λt, we get

In terms of decay rate we get R = R0e-λt
where R0 = λN0, decay rate at t = 0
(B) Half life (T1/2):
It is the time taken by radio nuclide to reduce half of its initial value.
half life period T1/2 = \(\frac{0.693}{\lambda}\)
Relation between (T1/2) and λ
If T1/2 is the half-life period, then N = \(\frac{\mathrm{N}_{0}}{2}\)
Substituting these values in N = N0e-λt, we get,
\(\frac{\mathrm{N}_{0}}{2}\) = N0e-λT1/2
2 = e-λT1/2
Taking log on both sides we get,
loge2 = λT1/2 (since log ex = x)

(C) Mean life(t) or average life:
It is defined as time taken by radio nuclei to reduce 1/eth of its initial value.
Mean life τ = \(\frac{1}{\lambda}\)
proof
We know In (\(\frac{N}{N_{0}}\)) = -λt

∴ t = τ, N = \(=\frac{N_{0}}{e}\)
In(1/e) = -λτ
In(e) = λτ
In e = 1
1 = λτ
∴ τ = 1/λ
(D) Relation between τ and T1/2
T1/2 = 693τ
![]()
(E) Units of Radioactivity:
The SI unit for radio activity is Becquerel. One becquerel is one disinte¬gration per second. The traditional unit of activity is curie.
1 curie = 3.7 × 1010 Bq
2. Alpha Decay (α decay):
In α decay, mass number is reduced by 4 units and atomic number is reduced by 2 units.

Q-value
Q value is the energy released in nuclear reaction. The Q value or disintegration energy of a decay can be defined as the difference between the initial mass energy and final mass energy of decay products The Q value of a decay is expressed as
Q = (mx – my – mHe)c2
3. Beta decay (β – decay): There are two types of β decay
- β+ decay
- β– decay
a. β+ decay:
In β+ decay atomic number is reduced by 1 unit. But mass number remains unchanged.
![]()
In β+ decay, positron and neutrino are emitted. In β+ decay, conversion of proton into neutron, positron and neutrino takes place.
![]()
b. β– decay:
In β– decay, atomic number is increased by 1 unit. But mass number does not change.
![]()
In β– decay a neutron converts into proton emitting electron and antineutrino.

![]()
4. Gamma Decay:
The excited nucleus comes back to ground state by emitting gamma rays.
Eg:

5. Properties of α, β and γ:
Properties of α – particle:
- α -particles have a charge of +2e and a mass four times that of hydrogen atom.
- They are deflected by electric and magnetic fields.
- They affect photographic plates.
- They produce fluorescence and phosphorescence.
- They have a high ionizing power.
- They can penetrate very thin metal foils.
- The velocity is of the order of 107 m/s.
Properties of β – particles:
- β – particle is an electron.
- They are deflected by electric and magnetic fields.
- They can affect photographic plates.
- They can produce fluorescence and phosphorescence
- They have low ionization power.
Properties of γ – ray:
- γ – rays are electromagnetic waves.
- They have the speed of light.
- They have high penetrating power.
- They can affect photographic plates.
- They can produce fluorescence and phosphorescence.
- They have ionizing power.
- They are not deflected by electric and magnetic fields.
![]()
Nuclear Energy:
In the nuclear reactions, huge quantity of energy is released
1. Fission:
In nuclear fission, a heavier nuclei split into lighter ones releasing huge energy. When Uranium atom is bombarded with neutron, it breaks into intermediate mass fragments as shown.
![]()
Note:
- The energy released perfission of Uranium nucleus is 200MeV.
- The neutrons released per fission of Uranium nucleus is 2.5
- Controlled chain reaction (nuclear fission) is basic principle of nuclear reactor.
- Uncontrolled chain reaction results in explosion. This is the principle behind atom bomb.
A. Chain reaction:
The nuclear fission (of U238) produces extra neutrons. These extra neutrons may bombard with the neighboring Uranium atoms and make it to undergo nuclear fission.
This fission again produces more neutrons. This process continues like a chain. This was first suggested by Enrico Fermi.
2. Nuclear Reactor:
The controlled chain reaction produce a steady energy output. This is the basic of nuclear reactor.
The main components of nuclear reactor:

(i) Fissionable material or fuel:
The fissionable material is (23592U). Which is placed inside the core where the fission takes place.
(ii) Moderator:
It is used to slow down fast moving neutron. Commonly used moderators are water, heavy water (D2O), and graphite.
(iii) Reflector:
The core is surrounded by reflector to prevent the leakage.
(iv) Control rods:
Its purpose is to absorb neutron and hence to control reaction rate. It is made up of neutron-absorbing material like Cadmium.
![]()
(v) Coolant:
The energy released in the form of heat is continuously removed by coolant. It transfers heat to the working fluid.
The whole assembly is properly shielded to prevent radiation from coming out. The working fluid gets converted into steam by heat and it drive turbines and generate electricity.
A. Multiplication Factor (K)
Multiplication factor is a measure of growth rate of neutrons. For steady power operation, value of K should be 1. (called critical stage). If K > 1, reaction rate increases exponentially.
3. Nuclear Fusion – Energy Generation in stars:
In nuclear fusion lighter nuclei combine to form heavier nuclei releasing energy. Nuclear fusion is thermo nuclear reaction. It occurs at high temperature. At high temperature, particles get enough kinetic energy to overcome Coulomb repulsion.
Thermonuclear fusion is the source of energy in sun. The fusion inside sun involves burning of hydrogen into Helium.
![]()
![]()
4. Controlled Thermonuclearfusion:
In future, we expect to build up fusion reactors to generate power. For this to happen, the nuclear fuel must be kept at a temperature 108K.
At this temperature fuel exists in plasma state. The problem is that no container can stand such a high temperature. Several countries around world including India are developing techniques to solve this problem.