Plus One Physics Notes Chapter 6 Work, Energy and Power

Students can Download Chapter 6 Work, Energy and Power Notes, Plus One Physics Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus One Physics Notes Chapter 6 Work, Energy and Power

Summary
The Scalar Product

The scalar product (or) dot product of any two vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\) is defined as

Where ‘q’ is the angle between \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\)
Note: The dot product of A and B is a scalar quantity. Geometrical meaning of \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{B}}\)
We know \(\overrightarrow{\mathrm{A}}\) . \(\overrightarrow{\mathrm{B}}\) = ABcosθ
= A(Bcosθ)
= B(A cosθ)

Properties

Question 1.

Answer:

Work Energy Theory
Statement:
The change in kinetic energy of a particle is equal to the work done on it by the net force.
Proof:
We know v² = u² + 2as
v² – u² = 2as
Multiplying both sides with m/2; we get

Work
Definition:
The work done by the force is defined as the product of component of the force in the direction of the displacement and the magnitude of this displacement.
Explanation


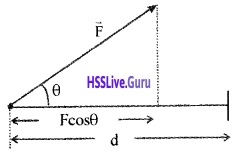
Consider a constant force \(\overrightarrow{\mathrm{F}}\) acting on an object of mass m. The object undergoes a displacement d in the positive x direction as shown in the figure. The projection of \(\overrightarrow{\mathrm{F}}\) on d is Fcosθ.
Hence work done w = Fcosθ. d

There are three types of workdone

1. positive workdone
2. negative workdone
3. zero workdone

1. Positive workdone:
Work will be positive, if the displacement has a component in the direction of the force. The angle between force and displacement is zero for positive workdone.
When q = 0 w = Fd
Example

• A person carrying a load climbing up a staircase
• A body being pushed along a surface
• A body falling under gravitation force.

2. Negative workdone:
Work will be negative, if the displacement has a component opposite to the force F. The angle between force and displacement lies between 90° and 180°.
Example

• When a person carrying a load on his head climbs down a staircase, (applied force by him on the load is upwards and the displacement is opposite to it)
• When a body slides along a rough surface the displacement is opposite to the frictional force. Therefore the workdone by the frictional force is negative.

3. Zero work done:
Work will be zero, if there is no component along the direction of force. The angle between applied force and displacement is 90°.
Example
1. When a person carrying a load on his head walks along a level road, the displacement is perpendicular to the force and therefore the work done is zero.

2. In uniform circular motion the centripetal force is along the radius and direction of displacement is along the tangent.

Kinetic Energy
Kinetic energy is the energy possessed by the body because of it’s motion. Kinetic energy of a body of mass m and velocity v,

Workdone By Variable Force

Consider a body moving from x_i to x_f under a variable force. The variation of force with position is shown in graph. Consider a small AB = Dx. The force in this interval is nearly a constant.

Hence workdone to move a body from A to B is. Dw = F(x) Dx.F(x)dx gives the area of rectangle ABCD. When we add successive rectangular areas, we get total work as

When we take Dx tends to zero, the summation can be replaced integration.

Work Energy Theory For A Variable Force
Work energy theorem for a variable force can be derived from work energy theorem of constant force. According work energy theorem for constant force, Change in kE = work done
dk = dw
dk = F dx
Integrating from the initial position (x_i) to (x_f) we get

Concept Of Potential Energy
Potential energy of a body is the energy possessed by it because of its position.
Explanation
Considera mass ‘m’on the surface of the earth. If this mass is raised to height ‘h’ against force of gravity,
work done w = Force × displacement
w = mg × h
w = mgh
This work gets stored as gravitational potential energy.
ie; Gravitational energy V = mgh.

1. Relation between gravitational potential and gravitational force:
If we take negative of the derivative of V(h) with respect to height (h), we get

Where F is gravitational force. The above equation shows that gravitational force is the negative derivative of gravitational potential.

2. Relation between kinetic energy and gravitational potential energy:
Considera body of mass ‘m’ at a height ‘h’ from the surface of the earth. The potential energy at height h
pE = mgh ______(1)
If the body is allowed to fall from this height, it attains kinetic energy,
kE = \(\frac{1}{2}\)mv² _______(2)
But velocity at surface can be found from the formula
v² = u² + 2as
v² = 2gh [Since u = 0, a = g, s = h]
Substituting this value in eq(2), we get
kE = \(\frac{1}{2}\) m2gh
kE = mgh
kE = pE [∵ pE = mgh]

Properties of conservative force:

• A force is conservative, if it can be derived from a scalar quantity (ie F = – \(\frac{d V}{d x}\))
• The workdone by the conservative force depends only on the end points.
• The workdone by conservative force in a closed path is zero.

Conservation of mechanical energy for a freely falling body:

Consider a body of mass ‘m’ at a height h from the ground.
Total energy at the point A
Potential energy at A,
PE = mgh
Kinetic energy, KE = \(\frac{1}{2}\)mv² = 0
(since the body at rest, v = 0).
∴ Total mechanical energy = PE + KE = mgh + 0
= mgh.

Total energy at the point B
The body travels a distance x when it reaches B. The velocity at B, can be found using the formula.
v² = u² + 2as
v² = 0 + 2 gx
∴ KE at B, = \(\frac{1}{2}\)mv²
\(\frac{1}{2}\)m2gx
= mgx
P.E. at B, = mg (h – x)
Total mechanical energy = PE + KE
= mg (h – x) + mgx = mgh.

Total energy at C
Velocity at C can be found using the formula
v² = u² + 2as
v² = 0 + 2gh
∴ KE at C, = \(\frac{1}{2}\)mv²
\(\frac{1}{2}\)m2gh
= mgh
P.E. at C = 0
Total energy = PE + KE
= 0 + mgh = mgh.

The Potential Energy Of A Spring
Hooks law:
The restoring force developed in the spring is proportional to the displacement x and it is opposite to the displacement,
ie Fα – x

Where k is a constant called the spring constant.
Potential energy stored in a spring:

Consider a massless spring fixed to a rigid support at one end and a body attached to the other end. The body moves on a frictionless surface.

If a body is displaced by a distance dx, The work done for this displacement
dw = Fdx
∴ Total work done to move the body from x = 0 to x


This workdone is stored a potential energy in a spring. Hence potential energy of a spring.

Spring force is a conservative force:
If the spring is displaced from an initial position x_i to x_f and again to x_i;

W = 0
This zero workdone means that spring force is conservative.
Energy of a oscillating spring at any point:

If the block of mass ‘m’ (attached to massless spring) is extended to x_m and released, it will oscillate in between +x_m and -x_m. The total mechanical energy at any point x, (lies between -x_m and +x_m) is

This block mass ‘m’ has maximum velocity at equilibrium equi¬librium position (x = 0). At this position, the potential energy stored in a spring is completely converted in to kinetic energy.

Graphical variation of energy

The Law Of Conservation Of Energy
Statement:
Energy cannot be created or destroyed. It can be transformed from one form to another.

Question 2.
Prove conservation of energy for a freely falling body.
Answer:
Conservation of mechanical energy for a freely falling body:

Consider a body of mass ‘m’ at a height h from the ground.
Total energy at the point A
Potential energy at A,
PE = mgh
Kinetic energy, KE = \(\frac{1}{2}\)mv² = 0
(since the body at rest, v = 0).
∴ Total mechanical energy = PE + KE = mgh + 0
= mgh.

Total energy at the point B
The body travels a distance x when it reaches B. The velocity at B, can be found using the formula.
v² = u² + 2as
v² = 0 + 2 gx
∴ KE at B, = \(\frac{1}{2}\)mv²
\(\frac{1}{2}\)m2gx
= mgx
P.E. at B, = mg (h – x)
Total mechanical energy = PE + KE
= mg (h – x) + mgx = mgh.

Total energy at C
Velocity at C can be found using the formula
v² = u² + 2as
v² = 0 + 2gh
∴ KE at C, = \(\frac{1}{2}\)mv²
\(\frac{1}{2}\)m2gh
= mgh
P.E. at C = 0
Total energy = PE + KE
= 0 + mgh = mgh.

Various Form Of Energy
1. Heat:
Heat is a one form of energy, it is the internal energy of molecule.

2. Chemical energy:
Chemical energy arises from the fact that the molecules participating in the chemical reaction have different binding energies.

If the total energy of the reactants is more than the products of the reaction, heat is released and the reaction is said to be exothermic reaction. If the heat is absorbed in chemical reaction it is called endothermic.

3. Electrical energy:
The flow of electrons produce electric current.

4. The equivalence of mass and energy Mass and energy are equivalent and are related by the relation. E = mc², where C, the speed of light in. vacuum.

Question 3.
How much energy will be liberated, when 1 Kg. matter converts in to energy?
Answer:
Energy liberated E = mc²
E = 1 × (3 × 10⁸)²
= 9 × 10¹⁶J.

5. Nuclear energy:
Nuclear energy is obtained from the sun. In this case four light hydrogen nuclei fuse to form a helium nucleus, whose mass is less than the sum of the masses of the reactants. This mass difference (called the mass defect on) is the source of energy.

Power
Power is defined as the time rate at which work is done.

Expression for power in terms of F and V:
The work done (dw) by a force F for a displacement dr is


Where \(\overrightarrow{\mathrm{V}}\) is the instantaneous velocity when the force is \(\overrightarrow{\mathrm{F}}\).
Unit:
Unit of power is watt. 1 watt = 1J/S.
There is another unit of power, namely the horse power (hp)
1 hp = 746w
Kilowatt hour kwh:
Kilowatt hour (kwh) is the unit of energy used to mea-sure electrical energy. One kilowatt hour is the energy consumed in one hour at the rate of 1000 watts/ second.
1 kwh = 1000 watts × 60 × 60 seconds
= 3.6 × 106ws
1 kwh = 3.6 × 106J
Note : kwh is a unit of energy and not of power.

Collisions
There are two types of collisions.

1. Elastic collision
2. Inelastic collision

1. Elastic collision:
Elastic collision is one in which both momentum and kinetic energy are conserved.
Eg:

• collision between molecules and atoms
• collision between subatomic particles.

Characteristics of elastic collision:

• Momentum is conserved
• Total energy is conserved
• K. E. is conserved
• Forces involved during collision are conservative forces

2. Inelastic collision:
Inelastic collision is one in which the momentum is conserved, but KE is not conserved.
Example.

• Mud thrown on a wall
• Any collision between macroscopic bodies in every day life.

Characteristics of inelastic collision:

• Momentum is conserved
• Total energy is conserved
• K.E. is not conserved
• Forces involved are not conservative
• Part or whole of the KE is converted into other forms of energy like heat, sound, light etc.

2. Collisions in one Dimension:
If the initial velocities and final velocities of both the bodies are along the straight line, then it is called one dimensional motion.

Consider two bodies of masses m₁ and m₂ moving with velocities u₁ and u₂ in the same direction and in the same line. If u₁ > u₂ they will collide. After collision let v₁ and v₂ be their velocities.
By conservation of linear momentum.
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ ______(1)
m₁u₁ – m₂u₂ = m₁v₁ – m₂v₂ ______(2)
This is an elastic collision, hence K.E. is conserved.

To find v₁ and v₂:


Discussion
Case -1 Mass of two bodies are equal
(i.e. m₁ = m₂ = m). Substitute these values in (7) and (8), we have

ie. bodies exchange their velocities.

Case – 2 (If u₂ =0 and m₂ >> m₁ ie; m₁ – m₂ ≈ -m₂, m₁ + m₂ ≈ -m₂)

The second body remains at rest while the first body rebounds with the same velocity.
Collisions in Two Dimensions:

Consider two bodies of masses m₁ and m₂ moving with velocities u₁ and u₂ along parallel lines. If u₁ > u₂ they will collide. Let v₁ and v₂ be their velocities after collision along directions θ₁ and θ₂. v₁ and v₂ can be resolved in to v₁ cosθ₁, v₂cosθ₂ parallel to x axis and v₁ sinθ₁ and v₂sinθ₂ parallel to y axis.
By conservation of momentum parallel to X-axis,

m₁u₁ + m₂u₂ = m₁v₁ cosθ₁ + m₂v₂ cosθ₂
By conservation of momentum parallel to y-axis.
m₁v₁sinθ₁ + m₂v₂ sinθ₂ = 0 + 0 = 0
By conservation of energy