Plus One Physics Notes Chapter 7 Systems of Particles and Rotational Motion

Students can Download Chapter 7 Systems of Particles and Rotational Motion Notes, Plus One Physics Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus One Physics Notes Chapter 7 Systems of Particles and Rotational Motion

Summary
Introduction
In the earlier chapters we discussed the motion of particle. We applied the results of our study to the motion of bodies of finite size.

A large class of problems with extended bodies can be solved by considering them to be rigid bodies. Ideally a rigid body is a body with a perfectly definite and unchanging shape. The distances between different pairs of particles of such a body do not change.

(i) Basically a rigid body can have two types of motion.

1. translational
2. Rotational motion

1. Translational motion:

In pure translational motion, at any instant of time every particle of the body has the same velocity. Explanation
Consider a rectangular block moving down along an inclined plane as shown in the figure: This body is rigid. Hence all the particles have same velocity. Any points like P1 or P2 of the body moves with the same velocity at any instant of time.

2. Rotational motion:
In pure rotational motion at any instant of time every particle of the body have different velocities. Explanation

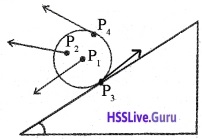
Consider a cylinder rolling down along inclined plane as shown in figure. Points P1, P2, P3 and P4 have different velocities (shown by arrows) at any instant of time.
Note: The above figure shows a combination motion of both translational and rotational motion.

Centre Of Mass
The centre of mass of a system of particles is the point where all the mass of the system may be assumed to be concentrated.
Position vector of two particle system:

Consider two particles of masses m1 and m2 with position vectors \(\vec{r}_{1}\) and \(\vec{r}_{2}\) respectively with respect to the origin O. Now the position coordinate of the center of mass C is defined as.

X, Y and Z coordinate of centre of mass of two particle system

Position vector of N particle system:
Consider a system of N particles of mass m₁, m₂…….,mN with position vectors \(\vec{r}_{1}, \vec{r}_{2}, \ldots \ldots \ldots \vec{r}_{N}\) respectively. Then the centre of mass of the system of N particle is defined as

Position vector of CM of continuous distribution of mass:
If body is continuous distribution of mass, we divide the body into n small elements of mass: Dm₁, Dm₂,………..DmN. Let r₁, r₂,……….rN be the position vectors of those small elements respectively.
Then position vector of CM is,

when we take N as bigger ((Dmi) becomes smaller) the summation can be changed into integration.

Motion Of Centre Of Mass
Velocity of centre of mass. The position vector of the centre of mass of N particle system is given

Differentiating the position vector of C.M., we get velocity of CM. ie;

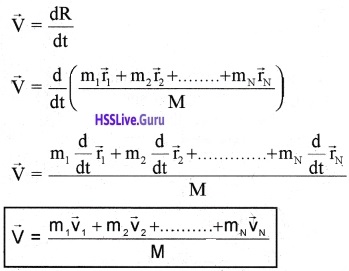
Acceleration of centre of mass:
Acceleration of centre of mass a = \(\frac{\mathrm{d}}{\mathrm{dt}} \overrightarrow{\mathrm{v}}\)

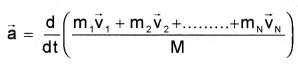
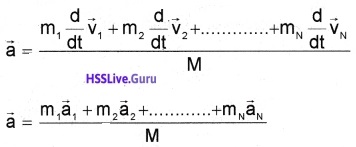
Force acting on the centre of mass:
Force acting on the centre of mass = Total mass at the centre of mass × acceleration of the centre of mass.
ie; \(\overrightarrow{\mathrm{F}}\) = M\(\overrightarrow{\mathrm{a}}\) ______(1)
But F = F_internal + F_extenal
By Newton’s third law, sum of the internal forces is zero.
∴ F = F_extenal
Therefore eq(1) becomes

Therefore the centre of mass moves as if it were a particle of mass equal to the total mass of the system and all the external forces are acting on it.

Linear Momentum Of A System Of Particles
Momentum of centre of mass
Velocity of centre of mass,

The equation means that, the total momentum of a system of particles is equal to the product of the total mass of the system and the velocity of its centre of mass.
Momentum conservation and centre of mass motion:
statement:
The total momentum of the centre of mass is conserved if no external force acts.
Proof:
According to Newton’s second law, rate of change momentum of centre of mass is directly proportional s to force acting on it.

If the total external force acting on the system is zero; the centre of mass moves with a constant velocity.
Application of the idea of centre of mass:

1. Explosion of a shell inflight

Consider a shell projected into air. If it is not exploded, its path will be a parabola. If it is exploded in air, the centre of mass follows the same parabolic path. Because the forces due to explosion are internal. Internal force can’t change the direction of centre of mass.
Note: External force can change the direction of centre of mass

2. Decay of radio active nuclei at rest:

Consider radioactive decay of radium nucleus moving along a straight line. A radium nucleus disintegrates into a nucleus of radon and an alpha particle. The two particles produced in the decay move in different directions. But the centre of mass (of radon and α particle) moves along a straight line, because the force leading to decay is internal. Internal force can’t change the direction of centre of mass.

Centre of mass frame:
If we observe this decay from the frame of reference in which the centre of mass (of a particle and radon) at rest, the product particle seems to be moving in opposite direction along a straight line.

In centre of mass frame, the motion of product particles become simple.

3. Binary stars:

Consider the trajectories of the two stars of equal mass as shown in figure. If there are no external forces, the centre of mass moves along a straight line as shown in figure.

Centre of mass frame of Binary stars:
If we look the trajectories of S₁ and S₂ from the centre of mass frame, we find that these two stars are moving in a circle as shown in figure.

In this frame of reference, the trajectories of the stars are a combination of

1. uniform motion in a straight line of the centre of mass and
2. circular orbits of the stars about the centre of mass.

Vector Product Of Two Vectors
The vector product of two vectors \(\overrightarrow{\mathrm{a}}\) and \(\overrightarrow{\mathrm{b}}\) is


Screw rule:
Rotate a right handed screw from \(\overrightarrow{\mathrm{a}}\) to \(\overrightarrow{\mathrm{b}}\). Then the direction of advance of the. tip of the screw gives the direction of (\(\overrightarrow{\mathrm{a}}\) × \(\overrightarrow{\mathrm{b}}\))

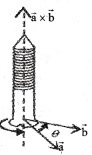
Right hand rule:
Curl the fingers of the right hand from \(\overrightarrow{\mathrm{a}}\) to \(\overrightarrow{\mathrm{b}}\) along the shorter angle. Then the direction in which the thumb points gives the direction of (\(\overrightarrow{\mathrm{a}}\) × \(\overrightarrow{\mathrm{b}}\)).

Properties of cross product:

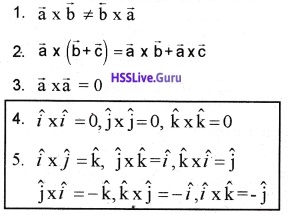
Note:
If \(\hat{i}, \hat{j}, \hat{\mathbf{k}}\) occur cyclically in the above vector product relation, the vector product is positive. If \(\hat{i}, \hat{j}, \hat{\mathbf{k}}\) do not occur in cyclic order, the vector product is negative.

Question 1.

Answer:

Angular Velocity And Its Relation With Linear Velocity
In earlier chapter, we treated angular velocity as scalar. But angular velocity is a vector quantity. The relation between angular velocity and linear velocity can be written in vector notation as

Direction of angular velocity:

Consider a body moving along the circumference of circle of radius ‘r’with velocity v. Then the direction of angular velocity will be perpendicular to both \(\overrightarrow{\mathbf{V}}\) and \(\overrightarrow{\mathbf{r}}\) (along the axis of rotation).

The figure(1) shows the direction of w, if body rotates in clockwise direction.

The figure(2) shows the direction of w, if body rotates in anticlockwise direction.
1. Angular acceleration:
Rate of change of angular velocity is called angular acceleration.
angular acceleration \(\vec{\alpha}=\frac{\mathrm{d} \vec{\omega}}{\mathrm{dt}}\)
If the axis of rotation is fixed, the direction of ω and hence α is fixed. In this case the vector equation reduces to scalar equation.

Torque And Angular Momentum
Torque and angular momentum are important quantities to discuss the motion of rigid bodies.

1. Moment of force (Torque)
Torque (or the moment) of a force of about a point is the rotating effect of the force about that point.
Explanation

If f is the force acting at a point A, then torque about a point O is given by


Where \(\overrightarrow{\mathbf{r}}\) is the position vector of the point A from the point O. Torque is a vector quantity. The direction of torque is (given by right hand screw rule). Perpendicular to both \(\overrightarrow{\mathbf{r}}\) and \(\overrightarrow{\mathbf{f}}\).
Unit:
The unit of torque is Nm.
Note:

• If the turning tendency of the force is anticlockwise, then the torque is positive and if it is clockwise, then torque is negative.
• Torque has dimensions ML²T^-2. Its dimensions are the same as those of work or energy. Torque is. vector, while work is scalar.
• Torque plays the same role in rotational motion as force does in translational motion.

Couple:
Two equal and opposite forces, separated by a distance, constitute a couple.

Moment of couple (Torque):
The moment of couple is the product of either of the forces and the perpendicular distance between them.

Question 2.
The door is a rigid body which can rotate about a fixed axis passing through the hinges. What makes the door rotate?
Answer:
A force applied to the hinge line can’t produce any rotation. But a force of given magnitude applied at right angles to the door at its outer edge is most effective in producing motion. The rotational analogue of force is moment of force. It is also referred to as torque.

Question 3.
When you fix a handle on a door where do you fix it?
Answer:
You fix it in such a way that the torque is maximum. For this the lever arm must be maximum. So the handle is fixed as far away from the hinges as possible Note: A couple produces rotation without translation motion.

2. Angular momentum of a particle:
Angular momentum of a particle about a point is defined as the moment of its linear momentum about that point.
Explanation

Considers particle of mass ‘m’ and linear momentum \(\overrightarrow{\mathbf{p}}\) at a position \(\overrightarrow{\mathbf{r}}\) relative to the origin O. The angular momentum \(\overrightarrow{\mathbf{l}}\) of the particle can be written as (with respect to the origin O).

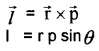
Note:

• The quantity angular momentum is the rotational analogue of linear momentum.
• Direction of \(\overrightarrow{\mathbf{l}}\) is given by right hand screw rule, (angular momentum is perpendicular to both \(\overrightarrow{\mathbf{r}}\) and \(\overrightarrow{\mathbf{p}}\)).

Relation between angular momentum and torque:
Angular momentum of a particle,

When differentiate on both side, we get


ie The rate of change of angular momentum is the torque applied to it. This is similar to force equal to rate of change of linear momentum.

Torque and angular momentum for a system of particles:
Consider a system having n particles. The total angular momentum of system is the vector sum of angular momentum of individual particles.
∴ total angular momentum of system,

\(\frac{\mathrm{dL}}{\mathrm{dt}}=\tau\) _____(1)
But Στ_i = τ is the total torque acting on the system of particle. Actually torque acting on a system is sum of external torque (τ_ext) and internal torque (τ_int)
ie. τ = τ_ext + τ_int
But τ_int = 0, because internal torque arises due to action – reaction pair. Action reaction pair for a system is zero.
∴ τ = τ_ext ______(2)
substituting eq(2) is eq (1) we get
\(\frac{\mathrm{d} \overrightarrow{\mathrm{L}}}{\mathrm{dt}}=\tau_{\mathrm{ext}}\)
The above equation means that, the time rate of the total angular momentum of a system of particles about a point is equal to the sum of the external torques acting on the system taken about the same point.

Conservation of angular momentum of a system:
For a system of particles,


If the total external torque on a system of particles is zero, then the total angular momentum of the system is conserved.
Note: The statement that the total angular momentum is conserved means that each of these three components (Lx, Ly, Lz) is conserved.

Equilibrium Of A Rigid Body
A rigid body is said to be in a mechanical equilibrium, if both it’s linear momentum and angular momentum are not changing with time.

(or)

A body is said to be in mechanical equilibrium, if the body has neither linear acceleration nor angular acceleration. A body moving with constant momentum is said to . be in translational equilibrium. Similarly a body with constant angular momentum is said to be in rotational equilibrium.

Condition for translational equilibrium:
If the total force acting on a rigid body is zero, the body, moves with constant linear momentum (or zero linear acceleration). The body moving with constant linear momentum is said to be in translational equilibrium Undertranslational equilibrium, the total force acting on the rigid body is zero.

Condition for rotational equilibrium:
If the total torque acting on rigid body is zero, the total angular momentum of the body does not change. Then the body is said to be in rotational equilibrium. Mathematical condition for rotational equilibrium is

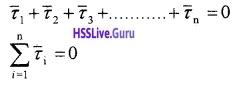
Principles of moments:

Consider a lever pivoted at some origin (say fulcrum) in mechanical equilibrium. Let \(\overrightarrow{\mathrm{f}}_{1}\) and \(\overrightarrow{\mathrm{f}}_{2}\) he the forces acting at A and B as shown in figure. Let \(\overrightarrow{\mathrm{R}}\) be the reaction of the support at the fulcrum. For translational equilibrium

For rotational equilibrium, sum of moments must be zero.
ie d₁f₁ + -d₂f₂ = 0
d₁f₁ = d₂f2₂ ______(2)
In the case of lever, f₁ is used to lift some weight. Hence f₁ is called load and its distance from the fulcrum d₁ is called load arm. Force f₂ is the effort applied to lift the load, distance d₂ is called effort arm.
Hence d₁f₁ = d₂f₂ can be written as
load arnn × load = effort arm × effort
The above equation expresses the principle of moments for a lever.
The ratio \(\frac{f_{1}}{f_{2}}\) is called mechanical advantage (MA)
Note:
High value of mechanical advantage means that a small effort can be used to lift a large load.
Examples for level

• See – saw
• Beam balance

1. Centre of gravity:
Centre of gravity of a body is that point through which the net gravitational force acts. The centre of gravity of a body may not be the same as its centre of mass. For a body of very large dimensions, the value of acceleration due to gravity is different for its different parts. In this situation the centre of gravity does not coincide with the centre of mass.

If the size of the body is small, the value of acceleration due to gravity is same for its different parts. In this situation, the centre of gravity of the body coincides with the centre of mass. Torque due to gravity.

Moment Of Inertia
A body at rest cannot rotate by itself. A body in uniform rotation cannot stop by itself. This inability of a material body is called rotational inertia. It depends on the mass of the body and axis of rotation. In other words it depends on a quantity called moment of inertia.

a. Moment of inertia of a particle:
Consider a particle of mass ‘m’ capable of rotation about an axis AB.

Let ‘r’ be the perpendicular distance of particle from AB. The moment of inertia of the particle about AB is defined as the product of mass of the particle and square of the distance between the particle and the axis of rotation.

b. Moment of inertia of a rigid body:

Consider a rigid body capable of rotation about an axis AB. Let the body consisting of particles of , masses, m₁, m₂, m₃……….m_n at distances r₁, r₂, r₃………..r_n
Then by definition, moment of inertia of m, about AB = m₁r₁².
M.I of m₂ about AB = m₂r₂²
————————–
M.I. of m_n about AB = m_nr_n²
Therefore total moment of inertia of the body about
I = m₁r₁² + m₂r₂² + ………………m_nr_n²

c. Moment of inertia of a ring about an axis through its centre and perpendicular to its plane:
Consider ring of mass M and radius R. AB the axis of rotation. Let ‘m’ be the mass of small section on the circumference of the ring.

M.I. of ‘m’about AB = mR²
∴ Total moment of inertia about AB,
I = ΣmR²

where Σm = M.

d. Moment of inertia of pair of small masses attached to the two ends of massless rod:
Consider a rigid massless rod of length / with a pair of small masses, rotating about an axis through the centre of mass perpendicular to the rod. Each mass M/2 is at a distance 1/2 from the axis of rotation.

∴ Total moment of inertia

Radius of gyration:
Radius of gyration of a body is the square root of ratio of moment of inertia and total mass of the body

Question 10.
Why do the concept of radius of gyration introduce?
Answer:
The moment of inertia of a body is given by
I = Σmr²
From the above equation it is clear that, we have to find the product of mass and the square of distances from the axis of rotation for all particles and then sum all these products. But the concept of radius of gyration simplifies the above problem.

In this method we find the centre of mass. Then we find a distance to any axis from this centre of mass, in such a way that the moment of inertia of this point (centre of mass) may be equal to that of I = Σmr². This distance from the axis of rotation to centre of mass is called radius of gyration. Practical utility of moment of inertia.

Question 11.
In a fly wheel (or) wheels of vehicles, most of the mass is concentrated at the rim? Explain why?
Answer:
(i) Flywheel:
The machines (such as steam engine, automobile engine etc) that produce rotational motion have a disc with large moment of inertia.

This disc is called fly wheel. Because of its large moment of inertia, the flywheel resists the sudden increase or decrease of the speed of the vehicle. It allows a gradual change in the speed and prevents the jerky motions. Thus fly wheel gives a smooth ride forthe passengers on the vehicle.

(ii) The wheels of vehicles:
The moment of inertia of wheels is increased by concentrating most of the mass at the rim of the wheel. If such a wheel gain or loses some K.E of rotation \(\left(\frac{1}{2} I \omega^{2}\right)\) brings a relatively smaller change in its angular speed w(∵ I is large) Hence such a flywheel helps in maintaining uniform rotation.

1. K.E of rotating body:
Consider a body rotating about an axis passing through some point O with uniform angular velocity ω. The body can be considered to be made up of a number of particles of masses m₁, m₂, m₃ etc.

At distances r₁, r₂, r₃ etc. All the particles will have same angular velocity ω. But their linear velocities will be different say v₁, v₂, v₃ etc.

Theorems Of Perpendicular And Parallelaxes
Theorem of perpendicular axes:
The moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with perpendicular axis lying in the plane of the body.

(or)

Moment of inertia of a plane lamina about the z-axis is equal to sum of the moments of inertia about x axis and the y axis, if planer lamina lies in xy plane.
Explanation

Let I_x and I_y be the moments of inertia of the lamina about ox and oy. Let I_z be the moment of inertia of the lamina about an axis perpendicular to the lamina and passing through ‘0’ (about z axis) Then by perpendicular axis theorem.

Question 12.
M.l of disc about one of its diameters.
Answer:
According perpendicular axis theorem, I_z = I_x + I_y
But in case I_x = I_y
I_z = 2 I_x _____(1)
But we know I_z = MR²/2 _____(2)
sub(2) in (1), we get \(\frac{\mathrm{MR}^{2}}{2}\) = 2 I_x
I_x = \(\frac{M R^{2}}{4}\)
The moment of inertia about any diameter is \(\frac{M R^{2}}{4}\).

1. Theorem of parallel axis:
The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.

Explanation
Let I be the moment of inertia of a-body about an axisAB. Let I0 be moment of inertia about the axis CD parallel to AB and passing through the centre of gravity (G of the body). Let M be the mass of the body and ‘a’ be the distance between the two axes. Then by parallel axes theorem.
I = I_o + Ma²

Question 13.
What is the moment of inertia of rod of mass M, length l about an axis perpendicular to it through one end.

Answer:
Consider a rod of mass M and length l, rotating about an axis passing through one end. Let d_x be a small element at a distance x from the axis of rotation.
mass of the element dx, dm = \(\frac{M}{l}\)dx
∴ M.I of length small element, dl = \(\frac{M}{l}\) dx x²

Moment of inertia of a ring about a tangent:
Consider a ring of mass M and radius R. If this ring is rotating about tangent, we can use parallel axis theorem.
According to parallel axis theorem,

Kinematics Of Rotational Motion About A Fixed Axis
The quantities ‘q’, w and ‘α’ in rotational motion has corresponding quantities in translational motion (x, ‘v’ and a respectively). For translational motion, we have
v = u + at
v² = u² + 2as
s = ut+ \(\frac{1}{2}\) at²
putting u = w₁, v = w₂ and s = q, we get the equations of motion in rotational motion.
w₂ = w₁ + αt
ω₂² = ω₁² + 2αθ
θ = ω₁t + \(\frac{1}{2}\) αt²

Dynamics Of Rotational Motion About A Fixed Axis
Table 7.2 lists quantities associated with linear motion and their analogues in rotational motion.
a. Work done by a torque:

Consider a particle at P₁. Let r₁ be the position vector at time t = 0. This position vector makes an angle q with x – axis. Let particle be acted by a force \(\overrightarrow{\mathrm{F}}_{1}\). Due to this force the particle subtends an angle dq and reaches at p₁¹.

ds is the linear displacement due to the force \(\overrightarrow{\mathrm{F}}_{1}\) This force makes angle with α₁, the position vector r₁.f₁ is the angle made by \(\overrightarrow{\mathrm{F}}_{1}\) with linear displacement.
Form the triangle the workdone for small displacement ds,

Substituting the eq(2) in (1) we get
dW₁ = τ₁dθ
For rigid body, there are many particles. Hence total work done on it.
dW₁ = (τ₁ + τ₂ +……….)dθ

Where τ is the total torque acting oh the body.

b. Rateofwork done by torque:
Instantaneous power due to torque.
We know dw = τ dθ
dividing both sides by dt, we have \(\frac{d w}{d t}=\tau \frac{d \theta}{d t}\)
P = τω

c. Angular acceleration:
Rate of change of angular velocity is called angular acceleration.
Angular acceleration α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\).

d. Relation between torque and angular acceleration:
The rate at which work is done on the body is equal to the rate at which kinetic energy increases.

τω = Iωα
τ = Iα
Note:
Just as force (F = ma) produces acceleration, torque produces angular acceleration in a body.
Newtons second law in rotation about a fixed axis

The angular acceleration is directly proportional to the applied torque and is inversely proportional to the moment of inertia of the body for rotation about a fixed axis.

Angular Momentum In Case Of Rotation About A Fixed Axis

Consider a rigid body rotating about a given axis with a uniform angular velocity w. Let the body consist of n particles of masses m₁, m₂, m₃…………m_n at perpendicular distances r₁, r₂, r₃………..r_n respectively from the axis of rotation.
If v₁, v₂, v₃…………v_n are the linear velocities of the
respective particles, then
v₁ = r₁w, v₂ = r₂w, v₃ = r₃w……….
The linear momentum of particle of mass m₁ is,
P₁ = m₁v₁
P₁ = m₁r₁w.
The angular momentum of this particle about the given axis,
l₁ = p₁ x r₁
= (m₁ v₁) x r₁
v₁ = r₁w
= m₁r₁²w
Similarly angular momentum of second particle
l₂ = m₂r₂²w
Angular momentum of the about the given axis,

1. Conservation of angular momentum:
Conservation of angular momentum and moment of inertia. When there is no external torque, the total angular momentum of a body or a system of bodies are a constant.

L = constant
But L = Iω
∴ Iω = a constant
Application

Question 14.
If the polar ice cap melts what will happen to the length of the day?
Answer:
For earth, angular momentum is a constant (Lw = constant, ie no torque acts on the earth). When the polar ice cap melts, the water thus formed will flow down to the equtorial region. The accumulation of water in equatorial line will increase the moment of inertia I of earth. In order to keep the angular momentum as a constant, w will decrease. The decrease in ‘w’ will increase the length of day.

Question 15.
If the earth loses the atmosphere what will happen to the length of the day?
Answer:
For earth, the angular momentum (L = Iw) is a constant, because there is no torque acting on it. When earth loses the atmosphere, I decreases and w increases to keep L as constant. Hence length of the day decreases.

Question 16.
A girl standing on a turn table. What happens to the rotation speed, if she stretches her hand?
Answer:
If a girl rotating with a uniform speed on turn table, it’s angular momentum (L = Iw) will be a constant. When she suddenly stretches her hand, I increases and w decreases to keep L as constant.

Question 17.
How does a circus acrobat and a divertake advantage of conservation of angular momentum?
Answer:
The diver while leaving the spring board, is throwing himself in a rotating, motion. When he brings his hands and legs close, I decrease and w increases. But before reaching water he will stretch his hands and legs. Hence I increases and w decreases. So that he gets a smooth entry into the water.

Rolling Motion

Question 18.
A wheel rolling uniformly along a level road is shown in the figure. The centre is moving with speed (V_CM). Find resultant velocities at P₁, P₂ and P₀.
Answer:
We know that the translational velocity of body is equal to the velocity of centre of mass. The velocity of centre of mass V_CM = Rw. Where R is the radius of wheel.
Velocity at P₁:
The point at P₁ has two velocities.

• Linear velocity (Vl)
• Translational velocity (Vt)

The linear velocity at P₁, V_l = Rw.
Translational velocity at P₁, V_t = Rw
[∵ translational velocities are same for all points on the wheel and its value equal to velocity of centre of mass].
The direction of V_l and V_t are same at P₁.
Hence total velocity at

Velocity at P₂:
Linear velocity at P₂, V_l = rw
[where r is the distance of P₂ from centre of mass]
translational velocity at P₂, V_t = Rw.
∴ Total velocity at

Velocity at P₀:
Linear velocity at P₀, \(\overrightarrow{\mathrm{V}}_{l}\) = Rω Translational at P₀, V_t = Rw.
The direction of V_land V_t are opposite.
∴ Hence total velocity,

= -Rw + Rw = 0
which means that the point P₀ is instantaneously at rest. Hence the friction at P₀ is zero. As a result rolling friction becomes less than the kinetic friction.
Note: The condition that P₀ is instantaneously at rest requires V_CM = Rw. Thus for the disc the condition for rolling without slipping is,
V_CM = RW.

1. Kinetic energy of rolling motion (without slipping):
In this case kinetic energy has two parts,

• due to the linear motion of centre of mass
• due to the rotational motion of the body.

K.E in terms of radius of gyration:
Moment of inertia I = mk²
where K is the radius of gyration of the body and v = Rw.
Substituting I, and V in eq(1), we get