Students can Download Chapter 4 Chemical Kinetics Notes, Plus Two Chemistry Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.
Kerala Plus Two Chemistry Notes Chapter 4 Chemical Kinetics
Chemical kinetics is the branch of chemistry which deals with the study of the velocity of chemical reactions and their mechanism.
Rate of a Chemical Reaction :
amount of chemical change per unit time.
Average Rate of Reaction:
change in concentration of any one of the reactants or products per unit time. Unit of rate of a reaction mol L-1 s-1 Fora reaction, R → P

Instantaneous Rate of Reaction:
the rate of change in concentration of any one of the reactants or products at a particular instant of time for a gven temperature. It may be expressed as \(\frac{dx}{dt}\) where dx is the change in concentration at the instant dt.
For the reaction aA + bB → cC + dD

Graphically,- instantaneous rate = slope of the tangent drawn to the concentration vs time graph
corresponding to the time t. i.e., rinst = \(\frac{dx}{dt}\) , where dx and dt are the intercepts.
![]()
Factors affecting rate of reaction:
Concentration of reactants, Nature of reactants and products, Temperature, Pressure (for gaseous reactants), Presence of catalyst, Presence of light (radiation)
Rate Expression and Rate Constant:
According to law of mass action, the rate of a chemical reaction is proportional to the product of molar concentrations of the reactants.
Consider a general reaction.
aA + bB → cC + dD
Rate α [A]x [B]y
where exponents ‘x’ and ‘y’ may or may not be equal to ‘a’ and ‘b’ respectively.
The above equation is also written as.
Rate = k[A]x [B]v
or \(\frac{-\mathrm{d}[\mathrm{R}]}{\mathrm{dt}}\) = k[A]x [B]v
where ‘k’ is a proportionality constant called rate constant. The equation is known as rate expression or rate law.
![]()
Rate law:
expression in which reaction rate is given in temis of molar concentration of reactants with each term raised to some power, which may or may not be same as the stiochiometric coefficient of the reacting species in a balanced chemical equation.
Order of Reaction :
sum of powers of the concentration of the reactants in the rate law expression. Considers general reaction,
aA + bB → cC + dD
Rate = k[A]x [B]v
Order = x + y
Example: H2 + l2 → 2 HI
Rate = k[H2]¹ [l2]¹, Order = 1 + 1 = 2
Order of a reaction is an experimentally determined quantity. It may be zero, whole number, fractional and even negative.
Elementary reactions –
reactions taking place in one step.
![]()
Complex reactions –
reactions involving a sequence of elementary reactions. These may be consecutive reactions, reverse reactions and side reactions.
Some example of reactions of different orders: First Order:
i) Decomposition of N2O5
N2O2 → 2NO2 + ½ O2
Or 2N2O5 → NO2 + O2
Rate = k[N2O5]¹
ii) Decomposition of NH4NO2 in aqueous solution.
NH4NO2 → N2 + 2H2O
Rate = k[NH4NO2]¹
Second order:
i. 2NO2 → 2NO + O2 Rate = k[NO2]²
ii. H2 + l2 → 2Hl Rate = k[H2]¹[l2]¹
Third order:
i. 2NO + O2 → 2NO2
Rate = k[NO]² [O2]¹
ii. 2NO2 + Cl2 → 2NOCl + O2
Rate = k[NO2]² [Cl2]¹

Units of Rate Constant:
For an nth order reaction, the unit of rate constant is given by the formula, mol1-n Ln-1 s-1
Molecularity of a Reaction :
number of reacting species (atoms, ions or molecules) taking part in an elementary reaction, which collide simultaneously in order to bring about a chemical reaction. It is always a whole number.
Reactions which involve simultaneous collision between two species are bimolecular.
![]()
When one reacting species is involved in the reaction, it is unimolecular.
Example:
NH4NO2 → N2 +2H2O
O3 → O2 + O
Reactions which involve simultaneous collision between two species are bimolecular.
Example:
2 Hl → H2 + l2
Reactions which involve simultaneous collision between three species are trimolecular or termolecular.
Example :
2 NO + O2 → 2 NO2
The probability that more than 3 molecules can collide and react simultaneously is very small. Hence, molecularity greaterthan 3 is not observed.
In a complex reaction, the slowest step in a reaction determine the rate of reaction, i.e., slowest step is the rate determining step.
Difference between order and molecularity
| Order | Molecularity |
| 1. It is sum of the powers of the concentration terms in the rate law expression. | 1. It is the number of reacting species undergoing simultaneous collision in the reaction. |
| 2. It is determined experimentally. | 2. It is a theoretical concept. |
| 3. It can be a whole number, zero or even fraction. | 3. It always a whole number. |
| 4. It gives some idea about reaction machanism. | 4. It does not tell us the reaction mechanism. |
Integrated Rate Equation :
Integrated rate equation gives a relation between concentrations at different times and rate constant.
Zero Order Reaction :
The rate of reaction is independent of the concentration of the reactants.
For a zero order reaction, R → P,
d[R] = – kdt
[R] = – kt + [R]0 ………….. (1)
or \(k=\frac{[R]_{0}-[R]}{t}\)
![]()
Equation (1) is of the form y = mx + c, equation for a straight line. If we plot [R] versus t, we get a straight line with slope = -k and intercept equal to [R]0
Note:
R0 initial concentration of reacting species (i.e., at time = 0)
R → concentration of reacting species (i.e., at time = t)
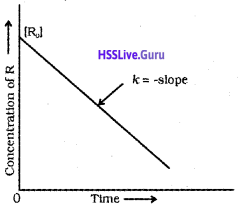
First Order Reaction
Fora reaction, R → P

If we plot a graph between log [R]<sub>0</sub>/[R] vs ‘t’ we get a straight line with slope = k/2.303

All natural and artificial radioactive decay take place by first order kinetics.
Half-Life of a Reaction (t½):
time required to reduce the concentration of a reactant to half of its initial concentration.
Forzero order reaction,
\(t_{1 / 2}=\frac{[R]_{0}}{2 k}\)
Derivation.
For a zero order reaction R → P, the rate constant is given by the equation,

Derivation:
For a first order reaction R → P, the rate constant is given by the equation,

For first order reactio t½ is independent of [R]0.
Pseudo First Order Reaction :
Reaction which appear to be of higher order but actually follow lower order kinetics.
Example:
Acid hydrolysis of ethylacetate.
![]()
Rate = k[CH3-COOC2H5]
Since the concentration of H2O is quite large and does not change appreciably, it does not appear in the rate law.
Another example: Inversion of cane sugar in presence of dilute acids.

Temperature Dependence of the Rate of a Reaction :
The rate of the reaction increases considerably with increase in temperature. For a chemical reaction with rise in temperature by 10°, the rate constant is nearly doubled.
![]()
Temperature Coefficient –
The ratio between the rate constant of a reaction at two temperatures differing by 10°.
Arrhenius Equation –
The temperature dependence of the rate of a chemical reaction can be explained by Arrhenius equation.
k = A e-Ea/RT
A → Arrhenius factor or frequency factor or pre-exponential factor
Ea → Activation energy in J mol-1
R → Gas constant
T → Temperature in kelvin
Activation energy (Ea)-
The energy required to form activated complex or intermediate. Some energy is released when the complex decomposes to form products.

Most probable kinetic energy –
kinetic energy of maximum fraction of molecules. The peak of the Boltzmann-Maxwell curve corresponds to this.

From the Arrhenius equation,
In k = In A \(\frac{E_{a}}{R T}\)
A polt of In k vs. \(\frac{1}{T}\)

If k1 and k2 are the rate constants at temperatures T1 and T2 respectively, Arrhenius equation can be written in the form,

Effect of Catalyst :
A catalyst is a substance which alters the rate of a reaction without itself undergoing any permanent chemical change. The function of a catalyst is to provide an alternate path of reaction with a lower energy of activation.

A small amount of the catalyst can catalyse a large amount of reactants. A catalyst does not alter Gibbs energy ∆ G of a reaction. It does not change the equilibrium constant but helps in attaining the equilibrium faster.
![]()
Collision Theory of Chemical Reactions :
It is based on kinetic theory of gases.
1. According to collision theory, the reactant molecules are assumed to be hard spheres and a chemical reaction takes place when reactant molecules collide with one another.
2. All collisions are not effective collisions. An effective collision is that collision which results into chemical reaction.
3. For effective collision, the molecule possess a certain minimum amount of energy called threshold energy and should have proper orientation.
Threshold energy – the minimum amount of energy which the colliding molecules must possess to make an effective collision.
4. Collision frequency (Z) – The number of collisions per second per unit volume of the reaction mixture.
5. To account for effective collisions, the probability or steric factor (P) is considered. It accounts for the fact that in a collision, molecules must be properly oriented.
Rate = PZABe-Ea/RT
Thus, in collision theory activation energy and proper orientation of the molecules together determine the criteria for effective collision and hence the rate of ’ reaction.