Plus Two Maths Chapter Wise Questions and Answers Chapter 2 Inverse Trigonometric Functions

Students can Download Chapter 2 Inverse Trigonometric Functions Questions and Answers, Plus Two Maths Chapter Wise Questions and Answers helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus Two Maths Chapter Wise Questions and Answers Chapter 2 Inverse Trigonometric Functions

Plus Two Maths Inverse Trigonometric Functions Three Mark Questions and Answers

Question 1.
Prove the following

Answer:

Question 2.
Find the value of

Answer:

Question 3.
If tan^-1x + tan^-1y + tan^-1z = π, show that x + y + z = xyz
Answer:
Given;
tan^-1x + tan^-1y + tan^-1z = π
⇒ tan^-1x + tan^-1y = π – tan^-1z

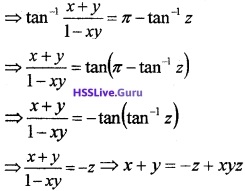
⇒ x + y + z = xyz.

Question 4.
Match the following

Answer:

Question 5.
Solve 2 tan^-1(cos x) = tan^-1(2 cos x)
Answer:
2 tan^-1(cosx) = tan^-1(2cosx)
⇒ \(\frac{2 \cos x}{1-\cos ^{2} x}\) = 2cosx
⇒ 1 = 1 – cos² x ⇒ 1 = sin²x
⇒ x = ±\(\frac{\pi}{2}\).

Question 6.
Solve the following

1. 2tan^-1(cosx) = tan^-1(2cosecx)
2. tan^-12x + tan^-13x = \(\frac{\pi}{4}\)

Answer:
1. 2tan^-1(cosx) = tan^-1(2cosecx)

2. tan^-12x + tan^-13x = \(\frac{\pi}{4}\)

⇒ (6x – 1)(x + 1) = 0
⇒ x = \(\frac{1}{6}\), x = – 1
Since x = – 1 does not satisfy the equation, as the LHS becomes negative. So x = \(\frac{1}{6}\).

Question 7.
Solve 2 tan^-1(cos x) = tan^-1(2 cos x)
Answer:
2 tan^-1(cos x) = tan^-1(2 cos x)
⇒ \(\frac{2 \cos x}{1-\cos ^{2} x}\) = 2cosx
⇒ 1 = 1 – cos² x
⇒ 1 = sin² x ⇒ x = ±\(\frac{\pi}{2}\)

Plus Two Maths Inverse Trigonometric Functions Four Mark Questions and Answers

Question 1.
Prove that \(\sin ^{-1} \frac{12}{13}+\cos ^{-1} \frac{4}{5}+\tan ^{-1} \frac{63}{16}=\pi\)
Answer:

Question 2.

1. Find the principal value of sec^-1\(\left(-\frac{2}{\sqrt{3}}\right)\) (1)
2. if sin\(\left(\sin ^{-1}\left(\frac{1}{5}\right)+\cos ^{-1}(x)\right)=1\), then find the value of x. (3)

Answer:
1. principal value of:

2. find the value of x:

Question 3.
Solve the following

Answer:

The value x = –\(\frac{\sqrt{3}}{\sqrt{28}}\) makes the LHS negative, so rejected.

Question 4.
(i) Choose the correct answer from the bracket. cos(tan^-1 x), |x| < 1 is equal to (1)


Answer:



(draw a right triangle to convert ‘tan’ to ‘sin’).

Question 5.
(i) In which quadrants are the graph of cos^-1 (x) lies, x ∈ [-1,1 ] (1)
(ii) If cos^-1x + cos^-1y = \(\frac{\pi}{3}\), then
sin^-1x + sin^-1y = ……… (3)
(a) \(\frac{2 \pi}{3}\)
(b) \(\frac{\pi}{3}\)
(c) \(\frac{\pi}{6}\)
(d) \(\frac{\pi}\)
(iii) If tan^-1x + tan^-1y = \(\frac{\pi}{4}\) then prove that x + y + xy = 1 (2)
Answer:
(i) First and Second quadrant


⇒ x + y = 1 – xy ⇒ x + y + xy = 1.

Question 6.
(i) sin(tan^-1(1)) is equal to


Answer:

Plus Two Maths Inverse Trigonometric Functions Six Mark Questions and Answers

Question 1.
Show that sin^-1\(\frac{3}{5}\) – sin^-1\(\frac{8}{17}\) = cos^-1\(\frac{84}{85}\).
Answer:


(draw a right triangle to convert ‘tan’ to ‘cos’).

Question 2.
(i) Choose the correct answer from the Bracket.
If cos^-1x = y, then y is equal to (1)
(a) π ≤ y ≤ π
(b) 0 ≤ y ≤ π
(c) \(-\frac{\pi}{2}\) ≤ y ≤ \(\frac{\pi}{2}\)
(d) 0 ≤ y ≤ π
(ii) Find the value of cos^-1 cos\(\left(\frac{7 \pi}{3}\right)\) (3)
(iii) Solve for x if, tan^-1\(\left(\frac{1+x}{1-x}\right)\) = 2 tan^-1x (2)
Answer:
(i) Range of cos^-1x is [0, π] ⇒ 0 ≤ y ≤ π

(ii) Here \(\left(\frac{7 \pi}{3}\right)\) lie outside the interval [0, π]. TO make it in the interval proceed as follows.