Plus Two Maths Notes Chapter 10 Vector Algebra

Students can Download Chapter 10 Vector Algebra Notes, Plus Two Maths Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus Two Maths Notes Chapter 10 Vector Algebra

Introduction
Physical quantities we deal are of two types, one that can be specified using a single real number which gives its magnitude and the other which involves the idea of direction as well as magnitude. The first type is called scalar quantity and the second is vector quantity. In this chapter we analyses the basic concepts about vectors, various operations, and their algebraic and geometrical properties.

I. Types of vectors

1. Equal Vectors: Vectors having same magnitude and direction regardless of the positions of their initial points.
2. Collinear Vectors: Vectors which are parallel to the same line, irrespective of their magnitude and direction.
3. Like and Unlike Vectors: Collinear vectors having same direction are like vectors and opposite direction are unlike vectors.
4. Unit Vectors: Vectors with magnitude unity.

II. Component form of a vector
Let i, j, k be the unit vectors along the x-axis, y-axis, z-axis respectively. The point P(x, y, z) be a point in space. Then the position vector of the point P can be expressed in component form as
1. If li + mj + nk is unit vector, then l,m,n are direction cosines along the vector.
2. If P (a, b, c) is a point on space, then a, b, c are direction ratios and

are direction cosines along the vector \(\overline{O P}\).

III. Addition of Vectors

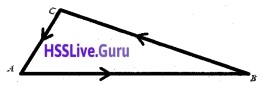
\(\overline{A B}+\overline{B C}+\overline{C A}=\overline{0}\) is known as triangle law of vector addition.

IV. Multiplication of a vector by a scalar
Let \(\bar{a}\) = a₁i + a₂j + a₃k be a vector and λ be a scalar. Then the product of the vector \(\bar{a}\) by a scalar is denoted by λ\(\bar{a}\) and the new vector formed has a magnitude λ|\(\bar{a}\)|.
λ\(\bar{a}\) = λa₁i + λa₂j + λa₃k

V. Vector joining two points
If P(a₁, a₂, a₃) and Q(b₁, b₂, b₃) are two points, then the vector joining P and Q is the vector \(\overline{P Q}\).
ie: \(\overline{P Q}\) = (b₁ – a₁)i + (b₂ – a₂)j + (b₃ – a₃)k

VI. Section Formula
If \(\bar{a}\) and \(\bar{b}\) be the position vectors of the points A and B respectively, then the position vector of the point P which divides AB in the ratio l:m

VII. Dot (Scalar) Product of vectors

VIII. Cross (vector) Product of Vectors

Geometrical meaning of vector product.

• \(\bar{a} \times \bar{b}\) is a vector perpendicular to \(\bar{a}\) and \(\bar{b}\).
• \(|\bar{a} \times \bar{b}|\) gives the area of a parallelogram with adjacent sides \(\bar{a}\) and \(\bar{b}\).

• i × i = j × j = k × k = 0,
• i × j = k, j × k = i, k × i = j
• j × i = -k, k × j = -i, i × k = -j

IX. Box (Scalar Triple) Product of Vectors

Properties:
1. Since \(\bar{b} \times \bar{c}\) is a vector, \([\bar{a} \bar{b} \bar{c}]\) is a scalar quantity.

2. |\([\bar{a} \bar{b} \bar{c}]\)| is the volume of the parallelopiped with a adjacent sides vector \(\bar{a}, \bar{b}, \bar{c}\).

3. If \(\bar{a}\) = a₁i + a₂j + a₃k; \(\bar{b}\) = b₁i + b₂j + b₃k and \(\bar{c}\) = c₁i + c₂j + c₃k, then

4. if \(\bar{a}, \bar{b}, \bar{c}\) be any three vectors, then \([\bar{a} \bar{b} \bar{c}]\) = \([\bar{b} \bar{c} \bar{a}]=[\bar{c} \bar{a} \bar{b}]\) (cyclic permutation of three vectors does not change the value of the scalar triple product).

5. In scalar triple product, the dot and cross can be interchanged.ie,

6. If any two vectors are interchanged the sign of box product is changed but magnitude remains the same.

7. If any two vectors are equal or proportional then the value of box product is zero.

8. Three vectors \(\bar{a}, \bar{b}, \bar{c}\) are coplanar if and only if \([\bar{a} \bar{b} \bar{c}]\) = 0.