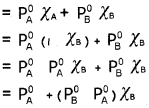Kerala State Board New Syllabus Plus Two Malayalam Textbook Answers Unit 1 Chapter 2 Prakasam Jalam Pole Anu Text Book Questions and Answers, Summary, Notes.
Kerala State Board New Syllabus Plus Two Malayalam Textbook Answers Unit 1 Eluttakam Text Book Questions and Answers, Summary, Notes.
Kerala State Board New Syllabus Plus Two Malayalam Textbook Answers Unit 3 Chapter 1 Kollivakkallathonnum Text Book Questions and Answers, Summary, Notes.
Kerala State Board New Syllabus Plus Two Malayalam Textbook Answers Unit 1 Chapter 4 Avakasangalude Prasnam Text Book Questions and Answers, Summary, Notes.
Kerala State Board New Syllabus Plus Two Malayalam Textbook Answers Unit 3 Chapter 2 Gauli Janmam Text Book Questions and Answers, Summary, Notes.
Kerala State Board New Syllabus Plus Two Malayalam Textbook Answers Unit 2 Chapter 4 Mappilappattile Keraleeyatha Text Book Questions and Answers, Summary, Notes.
Kerala State Board New Syllabus Plus Two Malayalam Textbook Answers Unit 1 Chapter 3 Kirathavritham Text Book Questions and Answers, Summary, Notes.
Kerala State Board New Syllabus Plus Two Malayalam Textbook Answers Unit 1 Chapter 1 Kannadi Kanmolavum Text Book Questions and Answers, Summary, Notes.
Kerala State Board New Syllabus Plus Two Malayalam Textbook Answers Unit 2 Chapter 3 Padathinte Pathathil Text Book Questions and Answers, Summary, Notes.
Kerala State Board New Syllabus Plus Two Malayalam Textbook Answers Unit 2 Chapter 2 Agnivarnante Kalukal Text Book Questions and Answers, Summary, Notes.
Kerala State Board New Syllabus Plus Two Malayalam Textbook Answers Unit 2 Chapter 1 Keshini Mozhi Text Book Questions and Answers, Summary, Notes.
Students can Download Chapter 3 Electrochemistry Notes, Plus Two Chemistry Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.
Electrochemistry-
branch of chemistry which deals with the inter-relationship between electrical energy and chemical changes.
Electrolysis – The chemical reaction occuring due to the passage of electric current (i.e., electrical energy is converted into chemical energy).
Electrochemical reaction –
The chemical reaction in which electric current is produced (i.e., chemical energy is converted into electrical energy). Example: Galvanic cell
Electrochemical Cell: – (Galvanic Cell/Voltaic Cell) :
It converts chemical energy into electrical energy during redox reaction, e.g. Daniell Cell
The cell reaction is
Zn(s) + Cu2+ (aq) Zn2+(aq) + Cu(s)
It has a potential equal to 1.1 V.
If an external opposite potential is applied in the Daniell ce|l, the following features are noted:
a) When Eext < 1.1 V,
(i) electrons flow from Zn rod to Cu rod and hence current flows from Cu rod to Zn rod.
(ii) Zn dissolves at anode and Cu deposits at cathode.
b) When Eext= 1.1 V,
(i) No flow of electrons or current,
(ii) No chemical reaction.
c) When Eext > 1.1 V
(i) Electrons flow from Cu to Zn and current flows from Zn to Cu.
(ii) Zn is deposited at the Zn electrode and Cu dissolves at Cu electrode.
Galvanic Cells :
In this device, the Gibbs energy of the spontaneous redox reaction is converted into electrical work.
The cell reaction in Daniell cell is a combination of the following two half reactions:
These reactions occur in two different vessels of the Daniell cell. The oxidation half reaction takes place at Zn electrode and reduction half reaction takes place at Cu electrode. The two vessels are called half cells or redox couple. Zn electrode is called oxidation half cell and Cu electrode is called reduction half cell. The two half-cells are connected externally by a metallic wire through a voltmeter and switch. The electrolyte of the two half-cells are connected internally through a salt bridge.
Salt Bridge :
It is a U-shaped glass tube filled with agar-agar filled with inert electrolytes like KCl, KNO3, NH4NO3.
Functions of Salt Bridge :
Electrode potential –
potential difference developed between the electrode and the electrolyte. According to IUPAC convention, the reduction potential alone is called electrode potential and is represented as \(E_{M^{n+} / M}\)
Standard Electrode Potential :
The electrode potential understandard conditions, (i.e., at 298 K, 1 atm pressure and 1M concentrated solution) is called standard electrode potential. It is represented as EΘ.
Representation of a Galvanic Cell :
A galvanic cell is generally represented by putting a vertical line between metal and electrolyte solution and putting a double vertical line between the two electrolytes connected by a salt bridge.
For example, the Galvanic cell can be represented as,
Zn (s)|Zn2+(aq)||Cu2+(aq)|Cu(s)
Cell Potential or EMF of a Cell :
The potential difference between the two electrodes of a galvanic cell is called cell potential (EMF) and is measured in volts.
EMF = Ecell = Ecathode – Eanode = ERjght – ELeft
Consider a cell, Cu(s) | Cu22+ (aq) || Ag+ (aq) | Ag(s)
Ecell = Ecathode – Eanode = EAg+/Ag – ECu2+/Cu
How to calculate emf of a cell when concentration varies from standard conditions.
Measurement of Electrode Potential using Standard Hydrogen Electrode (SHE)/Normal Hydrogen Electrode :
SHE or NHE consists of a platinum electrode coated with platinum black. The electrode is dipped in an exactly 1 M HCl solution and pure H2 gas at 1 bar is bubbled through it at 298 K. The electrode potential is arbitrarily fixed as zero at all temperatures.
Representation of SHE/NHE :
When SHE acts as anode:
Pt(s), Hsub>2(g, 1 bar) / H+(aq, 1 M)
When SHE acts as cathode:
H+(aq, 1 M)/H2(g, 1 bar), Pt(s)
Electrochemical Series/Activity series :
The arrangement of various elements in the increasing or decreasing order of their standard electrode potentials.
Applications of Electrochemical Series:
1. To calculate the emf of an electrochemical cell – The electrode with higher electrode potential is taken as cathode and the other as anode.
\(E_{\mathrm{cell}}^{\Theta}=E_{\mathrm{cathode}}^{\Theta}-E_{\mathrm{anodo}}^{\Theta}\)
2. To compare the reactivity of elements – Any metal having lower reduction potential (electode potential) can displace the metal having higher reduction potential from the solutions of their salt, e.g. Zn can displace Cu from solution.
Zn(s) + CuSO4(aq) → ZnSO4(aq) + Cu(s)
3. To predict the feasibility of cell reactions -If EMF is positive, the cell reaction is feasible and if it is negative the cell reaction is not feasible.
4. To predict whether H2 gas will be evolved by reaction of metal with acids – All the metals which have lower reduction potentials compared to that of H2 electrode can liberate H2 gas from acids.
5. To predict the products of electrolysis.
Nernst Equation :
It gives a relationship between electrode potential and ionic concentration of the electrolyte. For the electrode reaction,
Mn+ (aq) + n \(\overline { e } \) → M(s)
the electrode potential at any concentration measured with respect to SHE can be represented by,
R = gas constant (8.314 J K-1 mol-1), T=temperaturein kelvin, n = number of electrons taking part in the electrode reaction, F = Faraday constant (96487 C mol-1)
By converting the natural logarithm to the base 10 and subsitituting the values of R(8.314 J K-1 mol-1),T (298 K) and F (96487 C mol-1) we get,
Nernst Equation for a Galvanic Cell :
In Daniell cell, the electrode potential for any concentration of Cu2+ and Zn2+ ions can be written as,
Converting to natural logarithm to the base 10 and substituting the values of R, F and T=298 K, it. reduces to
Consider a general electrochemical reaction,
Equilibrium Constant and Nernst Equation:
where Kc is the equilibrium constant.
Electrochemical Cell and Gibbs Energy of the Reaction (∆rG):
Conductance of Electrolytic Solutions: .Conductors:
A substance which allows the passage of electricity through it. Conductor are classified as,
Metallic or Electronic Conductors:
In these the conductance is due to the movement of electrons and it depends on:
ii. Electrolytic Conductors
Electrolytes – The substances which conduct electricity either in molten state or in solution, e.g. NaCl, NaOH, HCl, H2SO4 etc. The conductance is due to the movement of ions. This is also known as ionic conductance and it depends on:
Ohm’s law – It states that the current passing through a conductor (I) is directly proportional to the potential difference (V) applied.
i.e., I ∝ V or I = \(\frac{V}{R}\)
where R – resistance of the conductor- unit ohm. In SI base units it is equal to kg m²/s³ A²
The electrical resistance of any substance/object is directly proportional to its length T, and inversly proportional to its area of cross section ‘A’.
R ∝ \(\frac{\ell}{\mathrm{A}}\) or R = ρ\(\frac{\ell}{\mathrm{A}}\) where,
ρ – (Greek, rho) – resistivity/specific resistance – SI unit ohm metre (Ω m) or ohm cm (Ω cm).
Conductance (G):
inverse or reciprocal of resistance (R).
\(G=\frac{1}{R}=\frac{A}{\rho \ell}=\kappa \frac{A}{\ell}\)
where K = \(\frac{1}{\rho}\) called conductivity or specific conductance (K – Greek, kappa)
SI unit of conductance – S (siemens) or ohm-1.
SI unit of conductivity – S m-1
1 S cm-1 = 100 S m-1
Molar Conductance of a Solution (Λm):
It is the conductance of the solution containing one mole of the electrolyte when placed between two parallel electrodes 1 cm apart. It is the product of specific conductance (K) and volume (V) in cm³ of the solution containing one mole of the electrolyte.
where M is molarity of the solution.
Unit of Λm is ohm’1 cm2 mol’1 Or S cm² mol-1
Λm = \(\frac{K}{C}\) [C-Concentration of the solution.]
Measurement of the Conductivity of Ionic Solutions :
The measurement of an unknown resistance can be done by Wheatstone bridge. To measure resitance of the electrolyte it is taken in a conductivity cell. The resistance of the conductivity cell is given by the equation.
\(R=\rho \frac{\ell}{A}=\frac{1}{\kappa A}\)
The quantity \(\frac{\ell}{\mathrm{A}}\) is called cell constant and isdenoted A by G*. It depends on the distance (/) between the electrodes and their area of cross-section (A).
Variation of Conductivity and Molar Conductivity with Concentration :
Conductivity (K) always decreases with decrease in concentration both for weak and strong electrolytes. This is because the number of ions per unit volume that carry the current in a solution decreases on dilution.
Molar conductivity (Λm) increases with decrease in concentration. This is because the total volume, V of the solution containing one mole of electrolyte also increases.
The variation of molar conductance is different for strong and weak electrolytes,
1. Variation of Λm with Concentration for Strong Electrolytes:
The molar conductance increases slowly with decrease in concentration (or increase in dilution) as shown below:
There is a tendency for Λm to approach a certain limiting value when concentration approaches zero i. e., dilution is infinite. The molar conductance of an electrolyte when the concentration approaches zero is called molar conductance at infinite dilution, Λm∞ or Λ°m. The molar conductance of strong electrolytes obeys the relationship.
Λm = Λ°m -AC1/2 where C = Molar concentration, A = constant for a particular type of electrolyte.
This equation is known as Debye-Huckel-Onsagar equation.
2. Variation of Λm with Concentration for Weak Electrolytes :
For weak electrolytes the change in Λm with dilution is due to increase in the degree of dissociation and consequently increase in the number of ions in total volume of solution that contains 1 mol of electrolyte. Here, Λm increases steeply on dilution, especially near lower concentrations.
Thus, the variation of Λm with √c is very large so that we cannot obtain molar conductance at infinite dilution Λ°m by the extrapolation of the graph.
Kohlrausch’s Law:
The law states that, the molar conductivity of an electrolyte at infinite dilution is equal to the sum of the molar ionic conductivities of the cations and anions at infinite dilution.
Λ°m = γ+ λ°+ + γ– λ°–
λ°+ and λ°– are the molar conductivities of cations and anions respectively at infinite dilution, Y+ and V. are number of cations and anions from a formula unit of the electrolyte.
Applications of Kohlaransch’s Law
1) To calculate Λ°m of weak electrolytes
2) To calculate degree of dissociation of weak electrolytes
\(\alpha=\frac{\Lambda_{m}}{\Lambda_{m}^{0}}\)
3) To determine the dissociation constant of weak electrolytes
Electrolytic Cell and Electrolysis:
In an electrolytic cell, external source of voltage is used to bring about a chemical reaction. Electrolysis is the phenomenon of chemical decomposition of the electrolyte caused by the passage of electricity through its molten or dissolved state from an external source.
Quantitative Aspects of Electrolysis
Faraday’s Laws of Electrolysis First Law:
The amount of any substance liberated or deposited at an electrode is directly proportional to the quantity of electricity passing through the
electrolyte.
w α Q where ‘Q’ is the quantity of electric charge in coulombs.
w = ZQ .
w = Zlt
(∵ Q = It) where T is the current in amperes , ‘t’ is the time in seconds and ‘Z’ is a constant called electrochemical equivalent.
Second Law:
The amounts of different substances liberated by the same quantity of electricity passing through the electrolytic solution are proportional to their chemical equivalent weights.
The quantity of electricity required to liberate/deposit 1 gram equivalent of any substance is called Faraday constant ‘F’.
1 F = 96487 C/mol ≈ 96500 C/mol
Products of Electrolysis:
It depend on the nature of the material being electrolysed and the type of electrodes being used.
Electrolysis of Sodium Chloride:
When electricity is passed through molten NaCl, Na is deposited at the cathode and Cl2 is liberated at the anode.
Na+(aq) + \(\overline { e } \) → Na(s) (Reduction at cathode)
Cl–(aq) → ½ Cl2(g) + \(\overline { e } \) (Oxidation at anode)
When concentrated aqueous solution of NaCl is electrolysed, Cl2 is liberated at anode, but at cathode H2 is liberated instead of Na deposition due to the high reduction potential of hydrogen.
The resultant solution is alkaline due to the formation of NaOH.
Electrolysis of CuSO4 :
When aqueous CuSO4 solution is electrolysed using Pt electrodes, Cu is deposited at the cathode and O2 is liberated at the anode.
Cu2+(aq) + 2 \(\overline { e } \) → Cu(s) (at cathode)
H2O(l) → 2H+(aq) + 1/2 O2(g) + 2 \(\overline { e } \) (at anode)
If Cu electrode is used, Cu is deposited at cathode and an equivalent amount of Cu dissolves in solution from the anode (because oxidation potential of Cu is higherthan that of water).
Cu2+(aq) + 2 \(\overline { e } \) → Cu(s) (at cathode)
Cu(s) → Cu2+(aq) + 2\(\overline { e } \) (atanode)
Commercial Cells (Batteries)
The electrochemical cells can be used to generate electricity. They are two types:
i) Primary Cells:
Cells in which the electrode reactions cannot be reversed by external energy. These cells cannot be recharged, e.g. Dry cell, Mercury cell.
ii) Secondary Cells :
Cells which can be recharged by passing current through them in the opposite direction so that they can be used again.
e.g. Lead storage battery, Nickel-Cadmium cell.
Primary Cells
a) Dry Cell:
Anode – Zn container
Cathode – Carbon (graphite) rod surrounded by powdered MnO2 and carbon.
Electrolyte – moist paste of NH4Cl and ZnCl2
The electrode reactions are :
Anode : Zn → Zn2+ + 2 \(\overline { e } \)
Cathode: MnO2 + NH4+ + \(\overline { e } \) → MnO(OH) + NH3
Dry cell has a potential of nearly 1.5 V.
b) Mercury Cell:
Anode – Zn amalgam (Zn/Hg)
Cathode – paste of HgO and carbon
Eelectrolyte – paste of KOH and ZnO. The electrode reactions are,
Anode : Zn/Hg + 2OH– → ZnO(s) + H2O + 2 \(\overline { e } \)
Cathode : HgO + H2O + 2 \(\overline { e } \) → Hg(l) + 2 OH–
Overall reaction : Zn/Hg + HgO(s) → ZnO(s)+ Hg(l)
The cell potential = 1.35 V
2. Secondary Cells
a) Lead Storage Battery :
Anode – lead plates
Cathode – grids of lead plates packed with lead dioxide (PbO2)
Electrolyte – 38% (by weight) soution of H2SO4.
The cell reactions when the battery is in use are,
Anode: Pb(s) + SO42-(aq) → PbSO4 + 2 \(\overline { e } \)
Cathode: PbO2(s) + SO42-(aq) + 4H+(aq) + 2 \(\overline { e } \) → PbSO4(s) + 2H2O(I)
The overall cell reaction is,
Pb(s) + PbO2(s) + 2H2SO4(aq) → 2PbSO4(s) + 2H2O(l)
The emf of the cell depends on the concentration of H2SO4. On recharging the battery the reaction is reversed and PbSO4(s) on anode is converted to Pb and PbSO4(s) at cathode is converted into PbO2.
b) Nickel-Cadmium Cell:
Anode- Cd
Cathode – metal grid containing nickel (IV) oxide. Electrolyte – KOH solution. The overall cell reaction during discharge is,
Cd(s) +2 Ni(OH)3(s) → CdO(s) + 2Ni(OH)2(s) + H2O(l)
3) Fuel Cells :
These are Galvanic cells designed to convert the energy of combustion of fuels directly into electrical energy.
H2 – O2 fuel cell – In this, hydrogen and oxygen are bubbled through porous carbon electrodes into concentrated aqueous NaOH solution, which acts as the electrolyte.
The electrode reactions are,
Anode : 2H2(g) + 4OH–(aq) → 4H2O(l) + 4\(\overline { e } \)
Cathode : O2(g) + 2H2O(l) + 4\(\overline { e } \) → 4OH–(aq)
Overall reaction : 2H2(g) + O2(g) → 2H2O(l)
Advantages of Fuel Cells –
pollution free, more efficient than conventional methods, Runs continuously as long as the reactants are supplied, electrodes are not affected.
Other examples:
CH4 – O2 fuel cell, CH3OH – O2 fuel cell
Corrosion :
Any process of destruction and consequent loss of a solid metallic material by reaction with moisture and other gases present in the atmosphere. More reactive metals are corroded more easily. Corrosion is enhanced by the presence of impurities, air & moisture, electrolytes and defects in metals.
Examples: Rusting of iron, tarnishing of Ag.
Mechanism:
In corrosion a metal is oxidised by loss of electrons to O2 and form oxides. It is essentially an electro chemical phenomenon. At a particular spot of an object made of iron, oxidation take place and that spot behaves as anode.
2 Fe(s) → 2 Fe2+ + 4\(\overline { e } \)E° = -0.44 V
Electrons released at anodic spot move through metal and go to another spot on the metal and reduce 02 in presence of H+. This spot behaves as cathode.
O2(g) + 4 H+(aq) + 4\(\overline { e } \) → 2 H2O(l) E° = 1.23 V
The overall reaction is,
2 Fe(s) + O2(g)+ 4H+(aq) → 2 Fe2+ + 2H2O(I) E° = 1,67V
The ferrous ions are further oxidised by atmospheric 02 to ferric ions and form hydrated ferric oxide (rust) Fe2O3.xH2O
Prevention of Corrosion
1) Barrier Protection:
Coating the surface with paints, grease, metals like Ni, Cr, Cu etc.
2) Sacrificial Protection:
Coating the surface of iron with a layer of more active metals like Zn, Mg, Al etc. The process of coating a thin film of Zn on iron is known as galvanisation.
3) Anti-rust Solutions:
Applying alkaline phosphate/ alkaline chromate on iron objects which provide a protectve insoluble film. Also, the alkaline nature of the solutions decreases the availability of H+ ions and thus decreases the rate of corrosion.
Students can Download Chapter 2 Solutions Questions and Answers, Plus Two Chemistry Chapter Wise Questions and Answers helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.
Question 1.
Which of the following is a liquid in solid type solution?
(a) glucose dissolved in water
(b) Camphor in N2
(c) amalgam of Hg with Na
(d) Cu dissolved in Au
Answer:
(c) amalgam of Hg with Na
Question 2.
The concentration term used when the solute is present in trace quantities is _______
Answer:
ppm (parts per million)
Question 3.
A binary solution of ethanol and n-heptane is an example of
(a) ideal solution
(b) Non-ideal solution with +ve deviation
(c) Non-ideal solution with -ve deviation
(d) unpredictable behaviour
Answer:
(b) Non-ideal solution with +ve deviation
Question 4.
A solution which has higher osmotic pressure as compared to other solution is known as _____
Answer:
Hypertonic
Question 5.
Which of the following solutions will have the highest boiling point at 1 atm pressure?
(a) 0.1M FeCl3
(b) 0.1MBaCl2
(c) 0.1MNaCl
(d) 0.1Murea
Answer:
(a) 0.1M FeCl3
Question 6.
1 kilogram of sea water sample contains 6 mg of dissolved O2. The concentration of O2 in the sample in ppm is
Answer:
6.0
Question 7.
The amount of solute (molar mass 60 g mol-1) that must be added to 180 g of water so that the vapour pressure of water is lowered by 10% is
Answer:
60 g
Pure Aqua provides users with an osmotic pressure calculator to gain better insight on your osmotic pressure requirements.
Question 8.
The correct equation for the degree of association (a) of an associating solute ‘n‘ molecules of which undergoes association in solution is
Answer:
a = \(\frac{n(i-1)}{1-n}\)
Question 9.
A solution is prepared by dissolving 10 g NaOH in 1250 ml of a solvent of density 0.8 ml/g. The molarity of the solution is _______
Answer:
0.25
Question 10.
If the elevation in boiling point of a solution of non volatile, non electrolyte in a solvent (Kb = xk. kg mol-1) is 7 K, then the depression in freezing point would be kf = ZK kg mol-1
Answer:
\(\frac{Y Z}{x}\)
Question 1.
Match the terms of list A with those in list B.
| A | B |
| Raoult’s Law. | Colligative property. |
| Henry’s Law. | Ideal solution. |
| Elevation of boiling point. | Solution of gases in liquids. |
| Benzene + Toluene. | Vapour pressure of solutions. |
Answer:
| A | B |
| Raoult’s Law. | Vapour pressure of solutions. |
| Henry’s Law. | Solution of gases in liquids. |
| Elevation of boiling point. | Colligative property. |
| Benzene + Toluene. | Ideal solution. |
Question 2.
At a particular temperature, the vapour pressure of two liquids A and B are 120 and 180 mm of Hg respectively. Two moles of A and 3 Moles of B are mixed to form an ideal solution. What is the vapour pressure for the solution?
Answer:
P°A = 120mm of Hg
P°B= 180 mm of Hg
χA = 2/5
χB =3/5
PA = P°A × χA
= 120 × 2/5 = 48 mm of Hg
PB = P°B × χB
= 180 × 3/5 = 108 mm of Hg
Ps = PA + PB
= 108 + 48 = 156 mm of Hg
Question 3.
Find the volume of H2O that should be added to 300 mL of 0.5 M NaOH so as to prepare a solution of 0.2 M.
Answer:
M1V1 = M2V2
300 × 0.5 = V2 × 0.2
V2 \(\frac{300 \times 5}{2}\) = 750 mL
H2O to be added = 750 mL – 300 mL = 450mL
Question 4.
Calculate the osmotic pressure of 5% solution of urea at 27°C?
Answer:
Mass of urea, WB = 5 g
R = 0.0821 L atm K-1 mol-1
T = 273 + 27°C = 300 K
Molecular mass of urea, MB = 60 g mol-1
V = 100 mL = 0.1L
= 20.53 atm
Question 5.
Osmotic pressure of 1M solution of NaCl is approximately double than that of 1M sugar solution. Why?
Answer:
Osmotic pressure is a colligative property and it depends on the number of solute particles present in the solution. In solution, each NaCl unit undergoes dissociation to form two particles (NaCl → Na+ + Cl–) and hence osmotic pressure of 1M NaCl is twice that of 1M sugar solution. Sugar molecules does not undergo association or dissociation in solution.
Question 6.
What do you mean by ideal solution?
Answer:
Ideal solution is a solution which obeys Raoult’s law over the entire range of concentration and temperature, i.e., for an ideal solution having two volatile components A and B.
PA = P°A χA, PB = P°B χB,
Ps = PA + PB =P°A χA + P°B χB
Question 7.
Many countries use desalination plants to meet their potable water requirements. Comment on the phenomenon behind it.
Answer:
This is based on reverse osmosis. When a pressure more than osmotic pressure is applied, pure water is squezed out of the sea water through a semi-permeable
Question 8.
Movement of solvent molecules through a semipermeable membrane from pure solvent to the solution side is called osmosis.
What are the following
Answer:
1. Isotonic solution:
If the osmotic pressure of the two solutions are equal, they are called isotonic solutions.
2. Hypertonic solution:
A solution having higher osmotic pressure than another solution is called hypertonic solution.
Question 9.
What is meant by azeotrope?
Answer:
Liquid mixtures which distil without change in composition are called azeotropic mixtures or azeotropes.
Question 1.
A student was asked to define molality. Then he answered that it is the number of gram moles of the solute dissolved per litre of the solution.
Answer:
Question 2.
The graph of non-ideal solution showing -ve deviation as drawn by a student is given below:
Answer:
As a result of this, vapour pressure of the solution decreases. Due to this, boiling point increases. The volume of the solution is less than the expected value. The mixing process is exothermic. So the actual graph is as given below:
Question 3.
Some words are missed in the following paragraph. Add suitable words in the blanks:
If osmotic pressure of 2 solutions are equal they are called ______(a)_____ solution. The solution which is having ______(b)______ osmotic pressure is called hypertonic solution and the solution which is having lower osmotic pressure is called ______(c)_____ solution.
Answer:
Question 4.
The solubility of gases depends upon some factors.
Answer:
Question 5.
A solution of 12.5 g of an organic solute in 170g of H2O a boiling point elevation of 0.63 K. Calculate the molecular mass of the solute (K2=0.52 K/m).
Answer:
Kb for water = 0.52 K Kg mol-1
WA = 170g
ΔTb = 0.63 K
WB = 12.5 g
MB = ?
Question 6.
Find the freezing point of the solution containing 3.6 g of glucose dissolved in 50 g of H20. (Kf for H2O = 1.86 K/m).
Answer:
Mass of glucose, WB = 3.6 g
Molecular mass of glucose = 180 g mol-1
Mass of solvent, WA = 50 g
Kf for H2O = 1.86 K/m = 1.86 K kg-1 mol-1
i.e., ΔTf = T°f – Tf= 0.744 K
∴ Freezing point of the solution, Tf = T°f – ΔT
= 273 K – 0.744 K = 272.3 K
Question 7.
Raw mangoes shrivel when pickled in brine solution.
Answer:
Question 8.
200 cm3 of an aqueous of a protein contains 1.26 g of the protein. The osmotic pressure of such a solution at 300 K is found to be 2.57 × 10-3 bar. Calculate the molar mass of the protein.
Answer:
Question 9.
What type of deviation from Rauolt’s law is exhibited by a mixture of phenol and aniline? Explain with the help of graph.
Answer:
Negative deviation.
In this case the intermolecular hydrogen bonding between phenolic proton and lone pair on nitrogen atom of aniline is stronger than the respective intermolecular hydrogen bonding between similar molecules. Thus, escaping tendency of the particles decreases in solution and hence the liquid mixture shows negative deviation.
Question 10.
Wilted flowers revive when placed in fresh water.
Answer:
1. Osmosis. It is the phenomenon of flow of solvent from pure solvent into a solution or from a solution of lower concentration into a solution of higher concentration through a semi-permeable membrane.
2. Negative deviation. Here chloroform molecule is able to form hydrogen bond with acetone molecule.
Thus escaping tendency of the particles decreases in solution and hence the liquid mixture shows negative deviation.
3. Benzoic acid undergoes association in solution.
2C6H5COOH \(\rightleftharpoons \) (C6H5COOH)2 Thus, the number of particles as well as colligative properties decreases. So molecular mass increases.
Question 11.
A solution is obtained by mixing 300 g of 25 % solution and 400 g of 40 % solution by mass. Calculate the mass percentage of the resulting solution.
Answer:
Mass of solute in 300 g of 25 % solution
\(\frac{300 \times 25}{100}\) = 75 g
Mass of solute in 400 g of 40 % solution
\(\frac{400 \times 40}{100}\) = 160 g
Total mass of solute = (75 + 160) g = 235 g
Total mass of solution = (300 + 400) g = 700 g
Mass % of solute in resulting solution = \(\frac{235 \times 100}{700}\) = 33.57%
Mass % of solvent (water) in resulting solution
= 100 – 33.57 = 66.43%
Question 12.
A graph showing vapour pressure against mole fraction of an ideal solution with volatile components A and B are shown below:
Answer:
Question 13.
Concentrated nitric acid used in the laboratory work is 68% nitric by mass in aqueous solution. What should be the molarity of such a sample of the acid if the density of the solution is 1.504 g mL-1?
Answer:
Question 14.
Why does gases always tend to be less solube in liquids as the temperature is raised?
Answer:
Dissolution of gases is exothermic process. It is because of the fact this process involves decrease of entropy (ΔS < 0). Thus, increase of temperature tends to push the equilibrium,
Gas + Solvent \(\rightleftharpoons \) Solution; ΔH = -ve
in the backward direction, thereby, supressing the dissolution.
Question 15.
The vapour pressure of water is 12.3 kPa at 300 K. Calculate vapour pressure of 1 molal solution of a non-volatile solute in it.
Answer:
P°H2O= 12.3 kPa
1000
In 1 molal solution, nsolute = 1; nH2O= \(\frac{1000}{18}\) = 55.5
∴ χH2O = \(\frac{55.5}{55.5+1}\)
Vapour pressure of the solution, Ps = P°H2O × χH2O
= 0.982 × 12.3 = 12.08 kPa
Question 16.
Determine the osmotic pressure of a solution prepared by dissolving 25 mg of K2SO4 in 2 litre of water at 25°C, assuming that it is completely dissociated.
Answer:
Since K2SO4 is completely dissociated as K2SO4 → 2K+ + SO42- Thus, i = 3
Osmotic pressure of the solution, π = i CRT
\(\frac{3 \times 25 \times 10^{-3} \mathrm{g} \times 0.0821 \mathrm{L} \mathrm{atm} \mathrm{K}^{-1} \mathrm{mol}^{-1} \times 298.15 \mathrm{K}}{174 \mathrm{g} \mathrm{mol}^{-1} \times 2 \mathrm{L}}\)
= 5.27 × 10-3 atm
Question 17.
Solution of sucrose is prepared by dissolving 34.2 g of it in 1000 g of water. Find out the freezing point of the solution, if Kf of water is 1.86 K/kg/mol? (Molecular mass of sucrose is 342 g/mol).
Answer:
ΔTf = kf × m
=1.86 K kg mol-1 × \(\frac{34.2 \mathrm{g} \times 1000 \mathrm{g} \mathrm{kg}^{-1}}{342 \mathrm{g} \mathrm{mol}^{-1} \times 1000 \mathrm{g}}\) = 0.186K
Tf = OK – 0.186 K
Freezing point of the solution = – 0.186 K
Question 18.
At 300 K, 36 g of glucose present in a litre of its solution has an osmotic pressure of 4.98 bar. If the osmotic pressure of the solution is 1.52 bars at the same temperature, what would be its concentration?
Answer:
In the first case, π1 = C1RT
i.e., 4.98 bar = \(\frac{36 \mathrm{g} \times \mathrm{R} \times 300 \mathrm{K}}{180 \mathrm{g} \mathrm{mol}^{-1}}\) ——– (1)
In second case, π2 = C2RT
i.e., 1.52 bar = C2R × 300 K ———- (2)
Question 19.
A solution containing 12.5 g of non-electrolytic substance in 175 g of water gave boiling point elevation of 0.70 K. Calculate the molecular mass of the substance? (Kb for water = 0.52 K kg mol-1)
Answer:
Molecular mass of the solute, MB = \(\frac{1000 \mathrm{K}_{\mathrm{b}} \mathrm{W}_{\mathrm{B}}}{\mathrm{W}_{\mathrm{A}} \Delta \mathrm{T}_{\mathrm{b}}}\)
\(\frac{1000 \mathrm{g} \mathrm{kg}^{-1} \times 0.52 \mathrm{K} \mathrm{kg}^{-1} \mathrm{mol}^{-1} \times 12.5 \mathrm{g}}{175 \mathrm{g} \times 0.70 \mathrm{K}}\)
= 53.06 mol-1
Question 20.
Answer:
Question 21.
Answer:
Question 22.
18 g of glucose is dissolved in 1kg of water in a beaker. At what temperature will water boil at 1.013 bar? (Kb for water is 0.52 K kg mol-1)
Answer:
Number of moles of glucose = 18/180 = 0.1 mol.
Mass of solvent = 1 kg.
Morality of glucose , m = \(\frac{n_{8}}{W_{A}}\)
= \(\frac{0.1 \mathrm{mol}}{1 \mathrm{kg}}\) = 0.1 mol/Kg
Elevation of boiling point ΔTb = Kb × m
= 0.52 K kg/mol × 0.1 mol/kg = 0.052 K
Since water boils at 373.15 K at 1.013 bar pressure, the boiling point of solution will be 373.15 K + 0.052 K = 373.202 K
Question 1.
Colligative properties are exhibited by dilute solutions.
Answer:
Question 2.
PA = P°A χA
PB = P°B χB
ΔmixV = O
Answer:
1. Ideal solutions.
2. Vapour pressure of a volatile component in the solution is the product of vapour pressure of pure component and mole fraction of that component in the solution.
3.
Question 3.
Answer:
1. The characteristics of a non-ideal solution
2.
Question 4.
Osmosis and osmotic pressure are two important terms related to solutions.
Answer:
1. The phenomenon of the spontaneous flow of a solvent from a solution of lower concentration to higher concentration, separated by a semipermeable membrane is called osmosis.
The excess hydrostatic pressure that builds up when the solution is separated from the solvent by a semipermeable membrane is called osmotic pressure.
2. Osmotic pressure (p) is proportional to the molar concentration/molarity (C) of the solution at a given temperature (T K).
π = CRT, where R is the gas constant.
π = \(\frac{n_{\mathrm{B}}}{V}\) RT, where nB is the number of moles of the solute and V is the volume of the solution in litres.
π V = nBRT
π V = \(\frac{w_{B}}{M_{B}}\)RT, where WB is the mass of the solute and MB is the molar mass of the solute.
Or MB = \(\frac{\mathrm{W}_{\mathrm{B}} \mathrm{RT}}{\pi \mathrm{V}}\)
Osmotic pressure measurement is widely used to determine molar mass of proteins, polymers and other macro molecules.
Question 5.
The value of molecular mass determined by colligative property measurement is sometimes abnormal.
Answer:
1. This is caused by dissociation in the case of KCl and association in the case of acetic acid. KCl in aqueous solution undergoes dissociation as KCl → K+ + Cl–
Molecules of ethanoic acid (acetic acid) dimerises in benzene due to hydrogen bonding. As a result of dimerisation the actual number of solute particles in solution is decreased. As colligative property decreases molecular mass increases.
Question 6.
The partial pressure of the gas in vapour phase is proportional to the mole fraction of the gas in the solution. This is the commonly used law for expressing the solubility of gas in liquid.
Answer:
1. Roult’s law.
For an ideal solution containing two volatile components A and B,
PA = P°A χA,
PB = P°B χB and
P[Total] = PA + PB = P°A χA + P°B χB
2. The factors affecting the solubility of a gas in a liquid:
Question 7.
Concentration of solution may be expressed in different ways.
Answer:
1. Molarity – It is the number of moles of the solute present in one litre of the solution.
2. Colligative properties are those properties which depends only on the number of solute particles.
3. ΔTb = Kbm
= \(\mathrm{k}_{\mathrm{b}} \frac{\mathrm{n}_{\mathrm{B}} \times 1000}{\mathrm{W}_{\mathrm{A}}}\)
i.e., ΔTb α nB i.e., elevation of boiling point depends on number of moles of solute. Hence, it is a colligative property.
Question 1.
Concentrated nitric acid used in the laboratory work is 68% nitric by mass in aqueous solution. What should be the molarity of such a sample of the acid if the density of the solution is 1.504 g mL-1?
Answer:
Question 2.
Why does gases always tend to be less solube in liquids as the temperature is raised?
Answer:
Dissolution of gases is an exothermic process. It is because of the fact this process involves decrease of entropy (ΔS < 0). Thus, increase of temperature tends to push the equilibrium,
Gas + Solvent \(\rightleftharpoons \) Solution; ΔH = -ve
in the backward direction, thereby, supressing the dissolution
Question 3.
The vapour pressure of water is 12.3 kPa at 300 K. Calculate vapour pressure of 1 molal solution of a non-volatile solute in it.
Answer:
P°H2O= 12.3 kPa
1000
In 1 molal solution, nsolute = 1; nH2O= \(\frac{1000}{18}\) = 55.5
∴ χH2O = \(\frac{55.5}{55.5+1}\)
Vapour pressure of the solution, Ps = P°H2O × χH2O
= 0.982 × 12.3 = 12.08 kPa
Question 4.
Determine the osmotic pressure of a solution prepared by dissolving 25 mg of K2SO4 in 2 litre of water at 25°C, assuming that it is completely dissociated.
Answer:
Since K2SO4 is completely dissociated as K2SO4 → 2K+ + SO42- Thus, i = 3
Osmotic pressure of the solution, π = i CRT
\(\frac{3 \times 25 \times 10^{-3} \mathrm{g} \times 0.0821 \mathrm{L} \mathrm{atm} \mathrm{K}^{-1} \mathrm{mol}^{-1} \times 298.15 \mathrm{K}}{174 \mathrm{g} \mathrm{mol}^{-1} \times 2 \mathrm{L}}\)
= 5.27 × 10-3 atm
Students can Download Chapter 2 Solutions Notes, Plus Two Chemistry Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.
Solutions:
homogeneous mixtures of two or more pure substances, having uniform composition and properties throughout. The substances forming a solution are called components.
Solvent and Solute:
The component that is present in the largest quantity is known as solvent.
One or more components present in the solution other than solvent are called solutes. e.g. In sugar solution, water is the solvent and sugar is the solute.
Binary solution:
A solution containing only two components.
Aqueous solutions:
solutions in which the solvent is water.
Types of Solutions
Percent Concentration. One way to describe the concentration of a solution is by the percent of the solution that is composed of the solute.
Expressing Concentration of Solutions :
The concentration of a solution is defined as the amount of solute present in the given quantity of the solution.
1. Mass percentage (w/w) :
The mass % of a component in a given solution is the mass of the component (solute) per 100 g of solution.
e.g. 10% glucose solution means 10 g of glucose dissolved in 90 g of water resulting in a 100 g solution.
2. Volume percentage (v/v) :
The volume % of a component in a given solution is the volume of the component per 100 volume of solution.
Example:
10% ethanol solution means 10 mL of ethanol dissolved in 90 mL of water.
3. Mass by volume percentage (w/v):
It is the mass of solute dissolved in 100 mL of the solution. Used in medicine and pharmacy.
4. Parts per million (ppm):
It is the parts of a solute (component) per million parts of the solution. When a solute is present in very minute amounts, parts per million (ppm) is used.
Use of Mole Fraction Equation … This formula is easy to use if you know the number of moles of all the solutes and solvents.
5. Mole fraction (X):
ratio of number of moles of one component to the total number of moles of all the components present in the solution.
For a binary solution, nA be the number of moles of A and nB be the number of moles of B.
The sum of mole fractions of all the components present in the solution is always equal to 1.
i.e., χA + χB = 1
Fora solution containing ‘i’ number of components,
χ1 + χ2 +……………… + χi = 1
Mole fraction is independent of temperature.
6. Molarity (M):
number of moles of solute dissolved in one litre of the solution.
7. Molality (m):
number of moles of solute per kilogram of the solvent.
Solubility:
Solubility of a substance is its maximum amount that can be dissolved in a specified amount of solvent at a particular temperature.
Factors affecting solubility
Nature of the solute, nature of the solvent, temperature ‘ and pressure
Solubility of Solids in Liquids :
Like dissolves like:
Polar solutes are soluble in polar solvents and non-polar solutes are soluble in non-polar solvents.
Unsaturated solution:
Solution in which more solute can be dissolved at the same temperature.
Saturated solution:
Solution in which no more solute can be dissolved at the same temperature and pressure.
Effect of temperature :
Solubility increases with temperature if the reaction is endothermic. Solubility decreases with temperature if the reation is exothermic.
Effect of pressure :
Pressure does not have any significant effect on solubility of solids in liquids because solids and liquids are highly incompressible and practically remain unaffected by changes in pressure.
Solubility of a Gas in a Liquid :
It is greately affected by pressure and temperature.
Effect of pressure
Henry’s law :
The law states that at a constant temperature, the solubility of a gas in a liquid is directly proportional to the pressure of the gas.
The most commonly used form of Henry’s law states that the partial pressure of the gas in the vapour phase (p) is proportional to the molefraction of the gas (χ) in the solution.
P = KH.χ
where KH is the Henry’s law constant.
Different gases have different KH values at the same temperature. Thus, KH is a function of the nature of the gas.
Higher the value of KH at a given pressure, the lower is the solubility of the gas in the liquid.
The solubility of gases increase with decrease of temperature. Therefore, aquatic species are more comfortable in cold waters rather than in hot waters.
Applications of Henry’s law
1. To increase the solubility of CO2 in soft drinks and soda water, the bottle is sealed under high pressure.
2. To avoid bends (a medical condition which is painful and dangerous to life caused by the formation of bubbles of N2 in the blood) the tanks used by scuba divers are filled with air diluted with He (11.7% He, 56.2% N2 and 32.1% O2).
3. At high altitudes, low pressure leads to low concentrations of O2 in blood. It causes climbers to become weak and unable to think clearly (anoxia).
Effect of temperature :
Dissoloution of gases in liquids is an exothermic process. Hence, according to Le Chatelier’s principle solubility of gases in liquids decreases with rise in temperature.
Vapour Pressure of Liquid Solutions
Vapour Pressure of Liquid-Liquid Solutions:
Consider the two volatile liquids denoted as ‘A’ and ‘B’. When both liquids are taken in a closed vessel, both components would evaporate and an equilibrium would be established between liquid and vapour phase.
Let, PA– Partial vapour pressure of component A’
PB – Partial vapour pressure of component ‘B’
χA Mole fraction of A
χB Moiefraction of B
Raoult’s Law :
The law states that fora solution of volatile liquids, the partial vapour pressure of each component in the solution is directly proportional to its mole fraction.
For component ‘A’
PA ∝ χA.
PA= P°A χA
where P°A is the vapour pressure of pure component ‘A’ at the same temperature.
Similarly, for component ‘B’
PB ∝ χB
PB= P°B χB
where PB° is the vapour pressure of pure component ‘B’. Rauolt’s law also states that, at a given temperature for a solution of volatile liquids, the partial vapour pressure of each component is equal to the product of the vapour pressure of pure component and its mole fraction.
According to Dalton’s law of partial pressures,
Total pressure, P[Total] = PA + PB
A plot of PA or PB versus the mole fractions χA and χB for a solution gives a linear plot as shown in the figure.
Raoult’s Law as a special case of Henry’s Law:
According to Raoult’s law, the vapour pressure of volatile liquid in a solution is proportional to its mole fraction, i.e., Pi = Pi° χi
According to Henry’s law, the vapour pressure of a gas in a liquid is proportional to its mole fraction, i. e., p=KHχ
Thus, Raoult’s law becomes a special case of Henry ’s law in which KH becomes equal to Pi°.
Vapour Pressure of Solution of Solids in Liquids:
If a non-volatile solute is added to a solvent to give a solution, the surface of solution has both solute and solvent molecules; thereby the fraction of surface covered by the solvent molecules gets reduced. Consequently, the number of solvent molecules escaping from the surface is reduced. Hence, the vapour pressure of solution is lower than vapour pressure of pure solvent.
General form of Raoult’s Law:
For any solution, the partial vapour pressure of each volatile component in the solution is directly proportional to its mole fraction.
In a binary solution, let us denote the solvent by ‘A’ and solute by ‘B’.
According to Raoult’s law,
PA ∝ χA
PA = PA° χA
Total pressure, P = PA Here, PB = 0
(∵ solute is non-volatile)
P = PA° χA
For binary solution,
χA + χB = 1
χA = 1 – χB
Thus, the above equation becomes,
lowering of vapour pressure.
Ideal and Non-ideal Solutions :
Ideal Solutions:
The solutions which obey Raoult’s law over the entire range of concentrations.
Important properties of Ideal Solutions
i. PA = P°A χA ; PB = P°B χB
ii. Enthalpy of mixing is zero (∆mixH = 0)
iii. Volume of mixing is zero (∆mixV = 0)
If the intermolecular attractive forces between A – A and B – Bare nearly equal to those between A – B, it leads to the formation of ideal solution.
Examples:
Non-ideal Solutions :
solutions which do not obey Raoult’s law overthe entire range of concentration. The vapour pressure of such solutions is either higher or lower than that predicted by Raoult’s law.
If the vapour pressure is higher, it exhibits positive deviation and if the vapour pressure is lower it exhibits negative deviation from the Raoult’s law.
Solutions showing positive deviation :
the intermolecular attractive forces between the solute- solvent molecules are weaker than those between the solute-solute and solvent-solvent molecules. Thus, in such solutions molecules will find it easier to escape than in pure state. This will increase the vapour pressure and results in the positive deviation.
(dotted line represents graph for ideal solution).
Examples:
Ethanol + Water, Ethanol + Acetone, CCl4 + Chloroform, C6H6 + Acetone , n-Hexane + Ethanol
Solution showing negative deviation:
In the case of negative deviation, the intermolecular attractive forces between solvent-solute molecules are greater than those between solvent-solvent and solute-solute molecules and leads to decrease in the vapour pressure.
Examples:
1. Mixture of phenol and aniline – In this case the intermolecular hydrogen bonding between phenolic proton and lone pair on nitrogen atom of aniline is stronger than the respective intermolecular hydrogen bonding between similar molecules.
2. Mixture of acetone and chloroform – Here chloroform molecule is able to form hydrogen bond with acetone molecule.
3. H2O + HCl, (4) H2O + HNO3, (5) CHCl3 + (C2H5)2O
Azeotropes:
binary mixtures having same composition in liquid and vapour phase and boil at a constant temperature. It is not possible to separate the components of azeotropes by fractional distillation.
Solutions which show large positve deviation from Raoult’s law form minimum boiling azeotrope at a specific composition. For example, ethanol-water mixture forms a minimum boiling azeotrope (b.p. 351.1 K) when approximately 95% by volume of ethanol is reached.
The solutions that show large negative deviation from Raoult’s law form maximum boiling azeotrope at a specific composition. For example, nitric acid and water form a maximum boiling azeotrope (b.p. 393.5 K) at the approximate composition, 68% nitric acid and 32% water by mass.
Colligative Properties :
properties which depend on the number of solute particles irrespective of their nature relative to the total number of particles present in the solution. These are,
i. Relative lowering of vapour pressure of the solvent \(\left(\frac{\Delta p_{1}}{p_{1}^{0}}\right)\)
ii. Elevation of boiling point of the solvent (∆Tb)
iii. Depression of freezing point of the solvent (∆Tf)
iv. Osmotic pressure of the solution (π)
Relative Lowering of Vapour Pressure:
When a non-volatile solute (B) is dissolved in a liquid solvent (A), the vapour pressure of the solvent is lowered. This phenomenon is called lowering of vapour pressure. It depends only on the concentration of the solute particles and it is independent of their identity. The relation between vapour pressure of solution, mole fraction and vapour pressure of the solvent is given as,
PA = χAP°A ……………(1)
The lowering of vapour pressure of solvent ∆ PA is given as,
∆ PA = P°A – PA ……………(2)
Substitute the equation (1) in (2)
∆ PA = P°A – P°AχA
= P°A(1 – χA)
∆ PA = P°AχB …………..(3) ∵ (1 – χA) = χB
The relative lowering of vapour pressure is given as,
of vapour pressure and is equal to the mole fraction of solute.
From equation (4),
For dilute solutions nB < < nA, hence neglecting nB In the denominator, the above equation becomes,
where wA and wB are the masses and MA and MB are the molar masses of solvent and solute respectively.
Elevation of boiling point (∆Tb):
The boiling point of a solution is higher than that of the pure solvent. The elevation in the boiling point depends ‘ on the number of solute molecules rather than on their nature.
Let T°b be the boiling point of pure solvent and Tb be the boiling point of solution. The increase in the boiling point ∆Tb = Tb – T°b is known as elevation of boiling point.
For a dilute solution, the elevation of boiling point ( ∆Tb) is directly proportional to the molal concentration of the solute in a solution (i.e., molality).
∆Tb ∝ m
∆Tb = Kbm …………(1)
where, m → molality and Kb → Boiling Point Elevation Constant/Molal Elevation Constant/ Ebullioscopic Constant.
Unit of Kb is K kg mol-1 Or K m-1
Substituting the value of‘m’ in equation (1),
Depression of Freezing point (∆Tf) :
The lowering of vapour pressure of a solution causes a lowering of the freezing point compared to that of the pure solvent.
Let T°f be the freezing point of pure solvent and Tf be the freezing point of solution.
Depression in freezing point ∆Tf= T°f – Tf
For a dilute solution, depression of freezing point (∆Tf) is directly proportioned to molality (m) of the solution. Thus,
∆Tf ∝ m
∆Tf = Kfm ………………(1)
where, Kf – Freezing Point Depression Constant/ Molal Depression Constant/Cryoscopic Constant.
Unit of Kf is K kg mol-1 Or K m-1
[Note: The values of Kb and Kf, depend upon the nature of the solvent. They Can be ascertained from the following equations:
where,
R → Gas constant, MA → Molar mass of solvent
Tb → Boiling point of pure solvent of kelvin
Tf → Freezing point of pure solvent in kelvin
∆fusH → Enthalpy of fusion, ∆vapH → enthalpy of vapourisation.
For water, Kb = 0.52 K kg mol-1 and Kf = 1.86 K kg mol-1]
Osmosis and Osmotic Pressure:
The process of flow of the solvent molecules from pure solvent to the solution through semipermeable membrane (SPM) is called osmosis.
Semi Permeable Membrane :
The membrane which allows the passage of solvent molecules but ’ not the solute molecule is called SPM.
Example:
Parchment paper, Pig’s bladder, Cell wall, Film of cupric ferrocyanide.
Osmotic Pressure (π):
the excess pressure which must be applied to a solution to prevent osmosis or the pressure that just stops the flow of solvent.
Osmotic pressure (π) is proportional to the molarity (C) of the solution at a given temperature (T K).
π = CRT, where R is the gas constant.
π = \(\frac{n_{B}}{V}\)RT, where nc is the number of moles of the solute and V is the volume of the solution in litres.
π = nBRT
π V= \(\frac{\mathrm{W}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{B}}}\)RT , where wB is the mass of the solute and MB is the molar mass of the solute.
Or MB = \(\frac{\mathbf{w}_{\mathrm{B}} \mathrm{RT}}{\pi \mathrm{V}}\)
Osmotic pressure measurement is widely used to determine molar mass of proteins, polymers and other macro molecules.
Advantages of osmotic pressure method:
i) pressure measurement is around the room temperature
ii) molarity of the solution is used instead of molality
iii) the magnitude of osmotic pressure is large compared to other colligative properties even for very dilute solutions.
Isotonic Solution :
Two solutions having same (equal) osmotic pressure at a given temperature. A 0.9% solution of NaCI (normal saline solution) is isotonic with human blood, and it is safe to inject intravenously.
Hypertonic Solution :
A solution having higher osmotic pressure than another solution.
Hypotonic Solution :
A solution having lower osmotic pressure than another solution.
Reverse Osmosis:
flow of the pure solvent from solution side to solvent side through semipermeable membrane when a pressure larger than the osmotic pressure is applied to the solution side.
Uses of reverse osmosis:
Desalination of sea water, Purification of water.
Abnormal Molar Mass :
In some cases, the molar mass determined by colligative properties do not agree with the theoretical values. This is due to association ordissociation of the solute particles in the solution.
Association of Solute Particles :
When solute particles undergo association the number of the solute particles in the solution decreases. Consequently, the experimental values of colligative properties are less than the expected values, e.g. Molecules of ethanoic acid (acetic acid) dimerise in benzene due to intermolecular hydrogen bonding.
Similarly, benzoic acid undergo dimerisation when dissolved in benzene.
Dissociation of Solute Particles :
When the solute particles dissociate or ionise in the solvent, the number of particles in solution increases and so the experimental values of the colligative properties are higher than the calculated values.
e.g. KCl in water ionises as
KCl → K+ + C–
Molar mass either lower or higher than the expected or normal value is called as abnormal molar mass.
van’t Hoff factor (i):
It accounts for the extent of association or dissociation.
Significance of van’t Hoff factor.
i > 1 ⇒ there is dissociation of solute particles.
i < 1 ⇒ there is association of solute particles.
i < 1 ⇒ there is no dissociation and association of solute particles.
Inclusion of van’t Hoff factor modifies the equations for colligative properties as follows:
Relative lowering of vapour pressure of solvent,
Students can Download Chapter 5 Surface Chemistry Notes, Plus Two Chemistry Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.
Surface chemistry deals with phenomena that occurs at the surfaces or interfaces.
Adsorption:
accumulation of molecular species at the surface rather than in the bulk of a solid or liquid, it is a surface phenomenon, e.g. Moisture gets adsorbed on silica gel.
Adsorbate:
molecular species or substance, which accumulates at the surface.
Adsorbent:
material on the surface of which adsorption takes place, e.g. Charcoal, Silica gel, etc.
Desorption:
process of removing adsorbed substance from the surface of adsorbent.
Difference between Adsorption and Absorption:
Adsorption –
the substance is concentrated only at the surface and does not penetrate to the bulk of the adsorbent.
Absorption –
the substance is uniformly distributed throughout the bulk of the solid, e.g. Moisture gets absorbed on anhydrous CaCl2 while adsorbed on silical gel.
Sorption:
term used when both adsorption and absorption take place simultaneously.
Mechanism of Adsorption :
The unbalanced or residual attractive forces are responsible for attracting the adsorbate particle on adsorbent surface. During adsorption energy decreases, therefore adsorption is exothermic process, i.e., ∆H of adsorption (heat of adsorption) is always negative. The entropy of the system also decreases (∆S = – ve).
Types of Adsorption:
1. Physical Adsorption (Physisorption):
Here the adsorbed molecules are held on the surface of the adsorbent by physical forces such as van der Waals’ forces. It is reversed by reducing pressure or by heating.
Characteristics:
Lack of specificity, easily liquifiable gases readily adsorbed, reversible in nature, extent of adsorption increases with increase in surface area of adsorbent, enthalpy of adsorption quite low (20 – 40 kJ mol’ ).
2. Chemical Adsorption (Chemisorption):
the forces of interaction between the adsorbent and adsorbate are chemical in nature. It cannot be easily reversed.
Characteristics:
High specificity, irreversibility, increases with increase in surface area, enthalpy of adsorption is high (80 -240 kJ mol”1).
Sometimes physisorption and chemisorption occur simultaneously and it is not easy to ascertain the type of adsorption. A physisorption at low temperature may pass into chemisorption as the temperature is increased. For example, dihydrogen is first adsorbed on Ni by van der Waals’forces. Molecules of hydrogen then dissociate to form hydrogen atoms which are held on the surface by chemisorption.
Comparison of Physisorption and Chemisorption
| Physisorption | Chemisorption |
| 1) Arises because of van der Waals’ force | 1) Caused by chemical bond formation |
| 2) Not specific | 2) Highly specific |
| 3) Reversable | 3) Irreversible |
| 4) More easily liquefiable gases are adsorbed readily. | 4) Gases which can react with the adsorbent show chemisorption. |
| 5) Enthalpy of adsorption is low (20-40 kJ mol’1) | 5) Enthalpy of adsorption is high (80-240 kJ mol-1) |
| 6) Low temperature is favourable. It decreases with increase of temperature | 6) Hig temperature is favourable. It increases with increase of temperature |
| 7) No appreciable activation energy is needed. | 7) High activation energy is sometimes needed. |
| 8) Increases with an increase of surface area. | 8) Increases with an increase of surface area. |
| 9) Results into multimolecular layers on adsorbent surface under high pressure. | 9) Results into unimolecular layer |
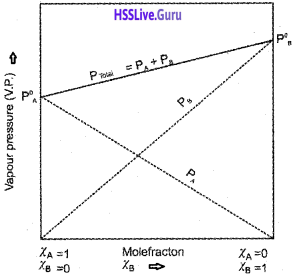
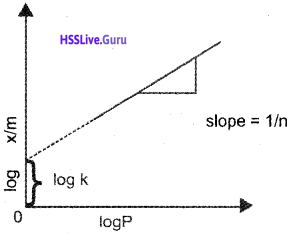
Adsorption Isotherms:
The variation in the amount of gas adsorbed by the adsorbent with pressure at constant temperature can be expressed by means of a curve termed as adsorption isotherm.
Freundlich Adsorption isotherm:
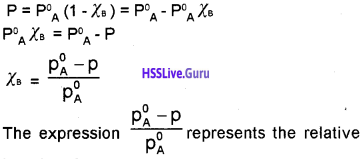
empirical relation between the quantity of gas adsorbed by unit mass of the solid adsorbant and pressure at a particular temperature.
x/m = k.P1/n (n > 1)
x → mass of the gas adsorbed
m → mass of adsorbent
‘k’ and ‘n’ are constants which depend on the nature of the adsorbent and the gas at a particular temperature.
OR log x/m = log k + \(\frac{1}{n}\) log P
Adsorption from Solution Phase:
Freundlich’s equation approximately describes the behaviour of adsorption from solution.
\(\frac{x}{m}\) = k.C1/n m
C – equilibrium concentration
log x/m = log k + \(\frac{1}{n}\) log C
Plotting log x/m vs log C a straight line is obtained
Applications of Adsorption:
Production of high vacuum, in Gas masks – activated charcoal is filled in gas mask to adsorb poisonous gases, for removal of colouring matter from solution in heterogeneous catalysis, in chromatographies analysis, in froth floatation process.
How to find Kp with the entropy and enthalpy amounts and with Gibb’s Free Energy.
Catalysis :
The process of altering the rate of chemical reaction by the addition of a foreign substance (catalyst) is called catalysis, e.g. MnO2 acts as a catalyst in the thermal decomposition of KClO3.
Promoters:
substances that enhance the activity of a catalyst, e.g. In Haber’s process, iron is used as catalyst and molybdenum acts as a promoter.
Poisons:
substances which decrease the activity of a catalyst.
Homogeneous and Heterogeneous Catalysis
a) Homogeneous Catalysis:
When the reactants and catalyst are in the same phase, the process is said to be homogeneous catalysis.
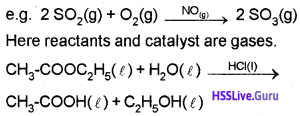
Here both the reactants and the catalyst are in the liquid phase.
Heterogeneous Catalysis:
If the reactants and the catalyst are in different phase, the catalysis known as heterogeneous catalysis.
Here reactants are gaseous state while the catalysts are in the solid state.
Important Features of Solid Catalysts
a) Activity:
ability of catalysts to accelerate a chemical reaction.
But pure mixture of H2 and O2 does not react at all in the absence of a catalyst.
b) Selectivity:
ability of a catalyst to direct a reaction to yield a particular product.
e.g. CO and H2 combine to form different products by using different catalysts.
Shape Selective Catalysis by Zeolites:
The catalytic reaction that depends upon the pore structure of the catalyst and size of the reactant and the product molecules.
Zeolites are good shape-selective catalysts because of their honey comb-like structures. Zeolites are widely used in petrochemical industries for cracking and isomerisation of hydrocarbon.
e.g. ZSM – 5 – which convert alcohols into petrol.
Enzyme Catalysis:
Enzymes are biological catalysts. They catalyse biological reaction in animals and plants to maintain life. e.g.
Characteristics:
Highly efficient, highly specific in nature, highly active under optimum temperature, highly active under optimum pH
Mechanism (Lock and key model)
The molecules of the reactant (substrate), which have complementary shape, fit into the cavities on the surface of enzyme particles just like a key fits into a lock. The enzyme catalysed reactions proceeds in two steps:
Step -1 :
Binding of enzyme to sutbstrate to form an activated complex.
E + S → ES*
Step-2 :
Decomposition of the activated complex to form product.
ES* → E + P
Catalysts in Industry
Colloids:
Heterogeneous system in which one substance is dispersed (dispersed phase) as very fine particles in another substance called dispersion medium, e.g. Starch, Gelatin. In colloids the particle size (diameter) is between 1nm and 1000 nm.
Classification of Colloids:
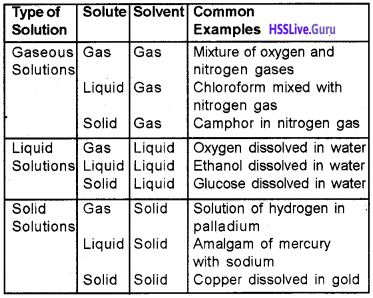
i) Based on physical state of dispersed phase and dispersion medium:
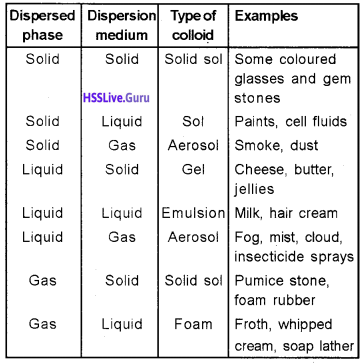
ii) Based on Nature of Interaction between Dispersed Phase and Dispersion Medium:
1. Lyophilic (solvent attracting) Colloids:
there is strong interaction between the dispersed phase and dispersion medium. They are reversible sols. e.g. Starch, gelatin, albumin etc.
2. Lyophobic (solvent repelling) Colloids:
there is little or no interaction between the dispersed phase and dispersion medium. They are also irreversible colloids and are not stable.
iii) Based on Types of Particle of the Dispersed Phase
a) Multimolecular Colloids :
the individual particles consist of an aggregate of atoms or small molecules with molecular size less than 1 nm, the particles are held together by van der Waals’ forces, e.g. Sulphur sol, Gold sol etc.
b) Macromolecular Colloids :
the particles of dispersed phase are sufficiently big in size, maybe in the colloidal range, e.g. Starch, cellulose, proteins.
c) Associated Colloids (Micelles):
colloids which behave as normal strong electrolytes at low concentration but get associated at higher concentrations and behaves as colloidal solutions. The associated particle formed are called micelles.
e.g. Soap, detergents etc.
The formation of micelles take place only above a particular temperature called Kraft temperature (Tk.) and above a particular concentration called Critical Micelle Concentration(CMC).
Mechanism of micelle formation –
In soaps, the RCOO– ions are present on the surface with their COO– groups in water and R staying away from it and remain at the surface. At CMC, the anions are pulled into the bulk of the solution and aggregate to form ‘ionic micelle’ having spherical shape with R pointing towards the centre of the sphere and COO– part remaining outward on the surface of the sphere.
Preparation of Colloids
a) Chemical Methods
Some examples:
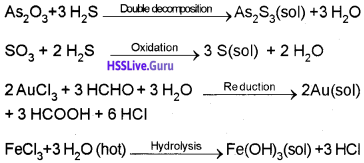
b) Electrical Disintegration or Bredig’s Arc Method
Metallic sols can be prepared by striking an arc between two electrodes of the metal, immersed in the dispersion medium. The metal is vapourised by the arc which then condenses to form particles of colloidal size. e.g. Gold sol, Platinum sol, Silver sol etc.
c) Peptization:
process of converting a precipitate into colloidal sol by shaking it with dispersion medium in the presence of small amount of electrolyte (peptizing agent), e.g. Freshly prepared Fe(OH)3 is peptized by adding small quantity of FeCI3 solution (peptizing agent).
Mechanism of peptization –
During peptization, the precipitate adsorbs one of the ions of the electrolyte on its surface. This causes the development of positive or negative charge on precipitates, which ultimately break up into smaller particles of the size of a colloid.
Purification of Colloids:
process of reducing the amount of impurities to a requisite minimum from the colloids.
i) Dialysis:
process of removing a dissolved substance from a colloid by means of diffusion through a suitable membrane.
ii) Electro-dialysis:
process of dialysis in presence of an applied electric field. It is faster and is applicable if the dissolved substance in the impure colloid is only an electrolyte. The ions present in the colloid migrate out to the oppositely charged electrodes.
iii) Ultrafilteration:
process of separating the colloidal particles from the solvent and soluble solutes present in the colloid by ultra filters. The ultra filter paper is prepared by soaking the filter paper in a colloidion solution (4% solution of nitro cellulose in a mixture of alcohol and ether). It is then hardened by formaldehyde and finally dried.
Properties of Colloids
1) Colligative Properties:
values of colligative properties as smaller due to smaller number of particles.
2) Tyndall Effect (Optical Property):
phenomenon of the scattering of light by colloidal particles.
Conditions for observing Tyndall effect:
1. The diameter of the dispersed particles is not much smaller than the wavelength of the light used; and
2. The refractive indices of the dispersed phase and the dispersion medium differ greatly in magnitude. The ultramicroscope used to observe the light scattered by colloidal particles is based on Tyndall effect.
The colour of the sky can be explained by Tyndall effect. The dust and other colloids present in the atmosphere scatter the light. Only blue light reaches to our eyes.
3) Colour:
It depends on the wavelength of lighty scattered by the dispersed particles which in turn depends on the size and nature of the particles and changes with the manner in which the observer receives the light, e.g. a mixture of milk and water appears blue when viewed by the reflected light and red when viewed by transmitted light.
4) Brownian Movement:
The constant zig-zag movement of the colloidal particles. It is due to the unbalanced bombardment of the particles by the molecules of the dispersion medium. It does not permit the particles to settle and is responsible for the stability of sols. ,
5) Charge on Colloidal Particles:
Colloidal particles carry an electric charge.
Positive charged sols: Al2O3. xH2O, CrO3.xH20, basic dye stuffs, blood (Haemoglobin) etc.
Negatively charged sols:
Metal sols (Cu, Ag, Au), metallic sulphides, acid dyes stuffs, starch, gelatin.
Reason for charge:
It is due to
i) electron capture by sol particles during electrodispersion of metals,
ii) preferential adsorption of ions from solution and/ or
iii) formulation of electrical double layer.
Helmholtz Electrical Double Layer:
combination of two layers of opposite charges around the colloidal particle. The first layer of ions is firmly held and is termed fixed layer while the second layer is mobile which is termed as diffused layer.
Electrokinetic Potential or Zeta Potential:
It is the potential difference between the fixed layer and the diffused layer of opposite changes in the electrical ‘ double layer.
Significance of Charge on Colloidal Particles:
provides stability to the colloid because the repulsive forces between charged particles having same charge prevent them from coalescing or aggregating when they come closer to one another.
6) Electrophoresis:
lled anaphoresis and that of cathode is called cataphoresis.
Coagulation/Flocculation/Precipitation:
process of settling of colloidal particles by the addition of electrolyte.
Coagulation of lyophobic sols can be carried out by the following ways:
Electrophoresis, mutual coagulation (mixing two oppositely charged sols), boiling, persistent dialysis, addition of electrolytes, etc.
Addition of electrolytes –
Colloids interact with ion carrying charge opposite to that present on themselves. This causes neutralisation leading to their coagulation.
Hardy – Schulze Rule:
the greater the valence of the flocculating ion added, the greater is its power to cause precipitation.
The ion having opposite charge to sol particles (coagulating ion) cause coagulation.
In the coagulation of negative sol, the flocculating power is in the order: Al3+ > Ba2+ > Na+
In the coagulation of positive sol, the flocculating power in the order:
[Fe(CN)6]4- > PO43- > SO42-> Cl–
Protective Colloids:
the lyophilic sol used for protection of lyophobic sol.
Emulsions:
liquidin liquid colloidal systems i.e., the dispersion of finely divided droplets in another liquid. There are two types of emulsions.
1) Oil dispersed in water (O/W type):
water acts as dispersion medium, e.g. Milk, Vanishing cream.
2) Water dispersed in oil (W/O type):
oil, acts as dispersion medium.e.g. Butter, Creams, Cod liveroil Emulsification – process of making an emulsion. Emulsion may be obtained by vigourously agitating a mixture of both liquids.
Emulsifying agent or emulsifier –
substance used to stabilise an emulsion. It forms an interfacial film between suspended particles and the medium, e.g.
Emulsifying agents for O/W emulsions :
Proteins, gums, natural and synthetic soaps etc.
Emulsifying agents for W/O emulsions:
Heavy metal salts of fatty acids, long chain alcohols, lampblack etc.
Colloids Around Us :
Fog, mist and rain; food materials, blood, soils, formation of delta.
Application of Colloids
I) In Medicine:
Colloidal medicines are more effective because they have large surface area and are, therefore, easily assimilated, e.g. Colloidal silver (Argyrol) – as eye lotion, Colloidal antimony – in curing Kalaazar, Colloidal gold – for intramuscular injection. Milk of magnesia – in stomach disorder.
II) In industries :
Electrical precipitation of smoke – by Cottrell smoke precipitator, purification of water, tanning, cleansing action of soaps and detergents (micelle formation), photographic plates and films, rubber industry and Industrial products.