Prasanna

Students can Download Chapter 7 Alternating Current Notes, Plus Two Physics Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus Two Physics Notes Chapter 7 Alternating Current

Alternating Current
AC current is commonly used in homes and offices. The main reason for preferring ac voltage over dc voltage is that ac voltages can be easily converted from one voltage to the other and can be transmitted over long distances. In this chapterwe will deal the properties of ac and its flowthrough different devices (inductor, capacitor, etc).

Ac Voltage Applied To A Resistor

Consider a circuit containing a resistance ‘R’ connected to an alternating voltage.
Let the applied voltage be
V = V_o sinωt ______(1)
According to Ohm’s law, the current at any instant can be written as
I = \(\frac{V_{0} \sin \omega t}{R}\)
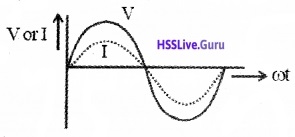
Where I₀ = V_o/R is the peak value of current. Comparing eq(1) and eq(2), we can understand that the current and voltage are in same phase.
Graphical variation of current and voltage:

R.M.S value (or Virtual value, effective value) of current and voltage:
The mean value of emf and current for one cycle is zero. Hence to measure ac, the root mean square (rms) values are considered.

The r.m.s value or virtual value of an AC is the square root of the mean of the squares of the instantaneous value of current taken over a complete cycle.
I_rms = \(\frac{I_{0}}{\sqrt{2}}\) and V_rms = \(\frac{V_{0}}{\sqrt{2}}\)
where I₀ – maximum current, V₀ – maximum voltage, (r.m.s.- root mean square).

Power dissipated in the resistor:
The average power consumed in one complete cycle,

Substituting current and voltage, We get

Representation Of Ac Current And Voltage By Rotating Vectors – Phasors
To represent the phase relation between current and voltage, phasors are used. Aphasoris a vector which rotates about the origin with an angular speed ω. The vertical components of phasors of V and I represent instantaneous value of V and I at a time t (see figure). The length of phasors give maximum amplitudes of V and I.

Phasor diagram of v and i for the circuit containing resistor only

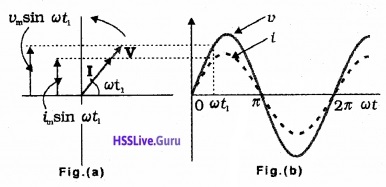
The figure(a) represent the voltage and current phasors and their relationship at time t₁. Fig (b) shows the graphical variation of V and I.

Ac Voltage Applied To An Inductor

Consider a circuit containing an inductor of inductance ‘L’ connected to an alternating voltage.
Let the applied voltage be
V = V_o sinωt _____(1)
Due to the flow of alternating current through coil, an emf, \(\frac{d I}{d t}\) is produced in the coil. This induced emf is equal and opposite to the applied emf (in the case of ideal inductor)

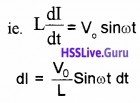
Integrating, we get

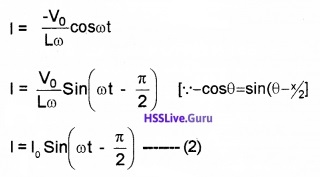
Where I_o = \(\frac{V_{0}}{L \omega}\),
The term Lω is called inductive reactance. Comparing eq(1) and eq(2), we can understand that, the current lags behind the voltage by an angle 90°.
Graphical variation of current and voltage:

Phasor diagram:

Inductive reactance X_L:
The resistance offered by an inductor to a.c. flow is called inductive reactance.
Inductive reactance

Power Consumed by an Inductor Carrying AC:
The instantaneous value of voltage and current in a pure inductor is
V = V_o sinωt
I = I_o cosωt
The average power consumed per cycle.

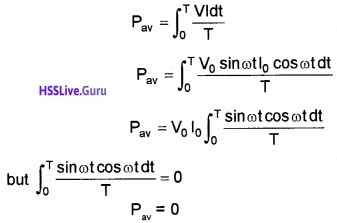
The above expression indicates that the average power or net energy consumed by an inductor carrying ac for a full cycle is zero.

Ac Voltage Applied To A Capacitor

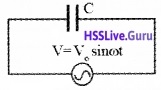
Consider a circuit containing a capacitor of capacitance ‘C’ connected to alternating voltage.
Let the applied voltage be V = V_o sinωt _____(1)
The instantaneous current through capacitor

Substituting eq.(1) in eq.(2), we get

\(\frac{1}{\mathrm{C} \omega}\) is called capacitative reactance
Comparing eq(1) and eq(3), we can understand that, the current leads the voltage by an angle 90°
Graphical variation of current and voltage:

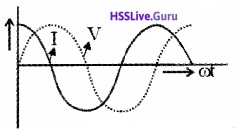
Phaser diagram:

Capacitative Reactance X_c:
The resistance offered by a capacitor to ac flow is called Capacitative reactance
Capacitative reactance

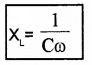
1. Power consumed by a capacitor carrying current:
The instantaneous value of voltage and current in a pure inductor is
V = V_o sinωt
I = I_o cosωt
The average power consumed per cycle.

The above expression indicates that the average power or net energy consumed by a capacitor carrying ac for a full cycle is zero.

Ac Voltage Applied To A Series Lcr Circuit

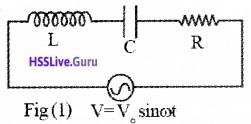
Consider a circuit containing an inductance L, resistance R and capacitance C connected in series. An alternating voltage V = V_o sinωt is applied to the circuit.
Phasor Diagram:

Let V_R be the voltage across R. This voltage is represented by a vector OA (since I and V_R are in same direction). Let V_L be the voltage across L. This voltage is represented by a vector OB (since the voltage V_L leads the current by angle 90°).

Similarly, let V_c be the voltage across C. This voltage is represented by a vector OC (since the voltage V_c lags the current by angle 90°).

The phase difference between V_L and V_c is Φ(ie. they are in opposite directions). So the magnitude of net voltage across the reactance is (V_L – V_c). This is represented by a vector OD in phasor diagram.

The final voltage in the circuit is the vector sum of V_R and (V_L – V_c). The final voltage is represented by diagonal OE.

1. Impedances of LCR circuit:
From the right angled triangle OAE,
Final voltage, V = \(\sqrt{\mathrm{V}_{\mathrm{R}}^{2}+\left(\mathrm{V}_{\mathrm{L}}-\mathrm{V}_{\mathrm{c}}\right)^{2}}\)

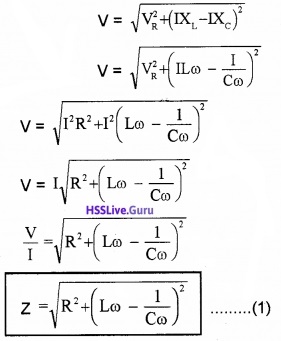
Where Z is called impedance of LCR circuit

Phase Difference: Let Φ be the phase difference between final voltage V and current I
From fig (2), we can write

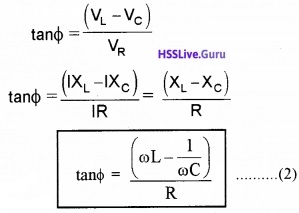
Expression for current:
The eq(2) shows that there is a phase difference between current and voltage. The instantaneous current lags the voltage by an angle (Φ).
If V = V_o sinωt is the applied voltage, the current at any instant can be written as
I = I_o sin(ωt – Φ) _____(3)
Where I_o is the peak value of current. It’s value can be written as

2. Analytical solution:
If we apply V = V_msinωt to an LCR circuit, we can write
V_L + V_R + V_C = V_m sinωt

Substituting these values in eq.(1), we get

The above equation (2) is like the equation for a forced, damped oscillator. Hence we can take the solution of above equation as
q = q_m sin(ωt + θ)

Substituting these values in eq.(2) we get

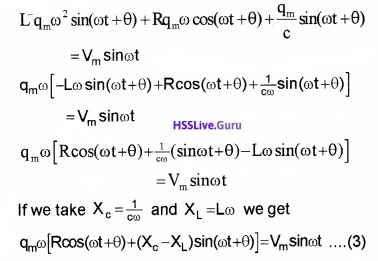
Multiplying and dividing by Z = \(\sqrt{R^{2}+\left(X_{0}-X_{L}\right)^{2}}\), we have

Substituting these values in eq.(4), we get
q_mωz[cosΦcos(ωt + θ) + sinΦsin(ωt + θ)] = V_msinωt
q_mωz cos(ωt + θ – Φ) = V_m sinωt ______(5)
(∴ cos(A – B) = cosA cosB + sinA sinB)
Comparing the two sides of the eq.(5) we get
V_m = q_mωz = i_mz
where i_m = q_mω
and cos(ωt + θ – Φ) = sinωt
sin (ωt + θ – Φ + π/2) = sinωt (∵ sin(θ + π/2) = cosθ)
ωt + θ – Φ + π/2 = ωt
(θ – Φ) = -π/2
Therefore, the current in the circuit is

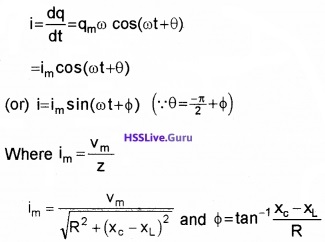
Thus, the analytical solution for the amplitude and phase of the current in the circuit agrees with that obtained by the technique of phasors.

3. Resonance:
When ωL = \(\frac{1}{\omega C}\), the impedance of the LCR circuit becomes minimum. Hence current becomes maximum. This phenomena is called resonance.

The frequency of the applied signal at which the impedance of LCR circuit is minimum and current becomes maximum is called resonance frequency.
Expression for resonance frequency
Resonance occurs at ωL = \(\frac{1}{\omega C}\)

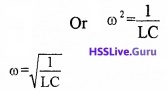
Impedance at resonance: Resonance occurs at ωL = \(\frac{1}{\omega C}\). Substituting this condition in eq(1), in section 7.6, we get
Impedance, Z = R
Current at resonance:
substituting ωL = \(\frac{1}{\omega C}\) in eq(2) in section 7.6 we get,
TanΦ = 0, or Φ = 0
Substituting this value in eq(3) in section 7.6, we get
current I= I_o sin ωt
Where I_o = V_o/R
Graphical variation of current with ω in LCR circuit:

Variation of current through LCR circuit with angular frequency co for two cases (1) R= 100Ω and (2) R=200Ω, is shown in the graph
Note: It is important to note that resonance phenomenon is exhibited by a circuit only if both L and C are present in the circuit. Only then the voltages across L and C cancel each other (both being out of phase).

The current amplitude ( V_m/R) is the total source voltage appearing across R. This means that we cannot have resonance in a RL or RC circuit.

4. Sharpness of resonance:

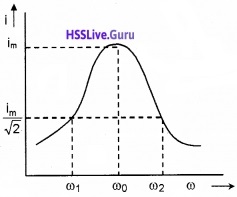
The figure shows the variation of current i with © in a LCR circuit.
Bandwidth: At ω₀, the current in the LCR circuit is maximum. Suppose we choose a value of ω for which the current amplitude is \(\frac{1}{\sqrt{2}}\) times its maximum value.

We can see that there are two values of ω(ω₁ and ω₂) and forwhich current is \(\frac{i_{m}}{\sqrt{2}}\).

The difference ω₂ – ω₁ is called bandwidth.
If we take ω₁ = ω₀ – ∆ω and ω₂ = ω₀ + ∆ω
We get bandwidth, ω₂ – ω₁ = 2∆ω.

Expression for bandwidth and sharpness of resonance:
We know that the current in the LCR circuit

We know that the current in the LCR circuit becomes \(\frac{i_{m}}{\sqrt{2}}\) at ω₂ = ω₀ + ∆ω. Substituting this m in eq(1), we get

But ω₂ = ω₀ + ∆ω, substituting this above equation.

Sharpness of resonance: The quantity \(\left(\frac{\omega_{0}}{2 \Delta \omega}\right)\) is
called sharpness of resonance.
From eq.(4),weget

When bandwidth increases, the sharpness of resonance decreases, ie. the tuning of the circuit will not be good.

Quality Factor (Q): The ratio \(\frac{\omega_{0} L}{R}\) is called the quality factor. When R is low or L is large, the quality factor becomes large. Lange quality factor means that the circuit is more selective.

Power in AC circuit: The power factor
Power in AC circuit with LC and R: In ac circuit the Voltage vary continuously.
∴ The average power in the circuit for one full cycle of period,


(since sin 2A = 2sinA CosA)
The mean value of sin²ωt over a complete cycle is 1/2 and the mean value of sin2ωt over a complete cycle is zero.

True power = Apparent power × power factor
The term P_av called true power. V_rms × I_rms is called the apparent power and cosΦ is called power factor.
powerfactor = \(\frac{\text { True power }}{\text { apparent power }}\)
Power factor is defined as the ratio of true power to apparent power.

Case – 1 (In purely resistive circuit)
In this case, current and voltage are in same phase. Hence Φ = 0
∴ P_av = V_rms I_rmsCosO
True power, P_av = V_rms I_rms

Case – 2 (In a purely inductive and purely capacitative circuit (no resistance)). In this case, the angle between voltage and current is 90°.
∴ P_av = V_rms I_rmsCos 90
True power, P_av = 0
Which means that, the power consumed by the circuit is zero. The current in such a circuit (purely inductive and purely capacitive) doesn’t do any work. A current that does not do any work is called wattles or idle current.

Lc Oscillations

A capacitor can store electrical energy. An inductor can store magnetic energy. When a charged capacitor is connected to an inductor, the electrical energy( of capacitor) transfers to magnetic energy (of inductor) and vise versa. Thus energy oscillates back and forth between capacitor and inductor. This is called L. C. Oscillations.
Expression for frequency:
Applying Kirchoff’s second rule, we get

Transformers
Principle: It works on the principle of mutual induction.
Construction:

A transformer consists of two insulated coils wound over a core. The coil, to which energy is given is called primary and that from which energy is taken is called secondary.

Working and mathematical expression :
Let V₁ N₁ be the voltage and number of turns in the primary. Similarly, let V₂, N₂ be voltage and number of turns in the secondary.

When AC is passed, a change in magnetic flux is produced in the primary. This magnetic flux passes through secondary coil.

If Φ₁ and Φ₂ are the magnetic flux of primary and secondary, we can write Φ₁ α N₁ and Φ₂ α N₂.
Dividing Φ₁ and Φ₂
\(\frac{\phi_{1}}{\phi_{2}}=\frac{N_{1}}{N_{2}}\)
[since Φ is proportional to number of turns] or \(\phi_{1}=\frac{\mathrm{N}_{1}}{\mathrm{N}_{2}} \phi_{2}\)
Taking differentiation on both sides we get

Step up Transformer:
If the output voltage is greater than input voltage, the transformer is called step up transformer. In a step up transformer N₂ > N₁ and V₂ > V₁.

Step down transformer:
If the output voltage is less than the input voltage, then the transformer is called step down transformer. In a step down transformer N₂ < N₁ and V₂ < V₁.

Efficiency of a transformer:
The efficiency of a transformer is defined as the ratio of output power to input power.

For an ideal transformer, efficiency = 1
i.e, V₁I₁ = V₂I₂

1. Power losses in a transformer
(i) Joule loss or Copper loss:
When current passes through a coil heat is produced. This energy loss is called Joule loss. It can be minimized by using thick wires.

(ii) Eddy current loss: This can be minimized by using laminated cores. Laminated core increases the resistance of the coil. Thus eddy current decreases.

(iii) Hysteresis loss: When the iron core undergoes cycles of magnetization, energy is lost. This loss is called hysteresis loss. This is minimized by using soft iron core.

(iv) Magnetic flux loss:
The total flux linked with the coil may not pass through secondary coil. This loss is called magnetic flux loss. This loss can be minimized by closely winding the wires.

Students can Download Chapter 6 Electromagnetic Induction Notes, Plus Two Physics Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus Two Physics Notes Chapter 6 Electromagnetic Induction

Introduction
In this chapter we are going to discuss the laws governing electromagnetic induction; how energy can be stored in a coil, generation of ac, the relation between voltage and current in various circuit components and finally the working of transformer.

The Experiments Of Faraday And Henry
Faraday and Henry conducted a series of experiments to develop principles of electro magnetic induction.
Experiment – 1

Connect a coil to a galvanometer G as shown in the figure. When the north pole of a bar magnet is pushed towards the coil, galvanometer shows deflection. The deflection indicates that a current is produced in the coil.

The galvanometer does not show any deflection when the magnet is held stationary. When the magnet is pulled away from the coil, the galvanometer shows deflection in the opposite direction.

Conclusion of experiment 1:
The relative motion between magnet and coil produces an electric current in the first coil.
Experiment 2

Connect a coil C₁ to a galvanometer G. Take another coil C₂ and connect it with a battery. A steady current in the coil produces a steady magnetic field. When the coil C₂ is moved towards the coil C₁, the galvanometer shows a deflection. This deflection indicates that the electric current is induced in the coil G.

When the coil C₂ is moved away, the galvanometer shows a deflection in the opposite direction. When the coil C₂ is kept fixed, no deflection is produced in the coil C₁.
Conclusion of Experiment – 2:
The relative motion between two coils induces an electric current in the first coil.
Experiment – 3

In this experiment coil C₁ is connected to galvanometer G. The second coil C₂ is connected to a battery through a key K.

When the key K is pressed, the galvanometer shows a deflection. If the key is held pressed continuously, there is no deflection in the galvanometer. When the key is released, a momentary deflection is observed again, (but in opposite direction).

Conclusion of experiment – 3:
The change in current in second coil induces a current in the first coil.

Magnetic Flux

Magnetic flux through a plane of area A placed in uniform magnetic field B can be written as

Φ = BAcosθ

Faraday’S Law Of Induction
Faraday’s law of electromagnetic induction states that the magnitude of the induced emf in a circuit is equal to the time rate of change of magnetic flux through the circuit.
Mathematically, the induced emf is given by

If the coil contain N turns, the total induced emf is given by,

Lenz’S Law And Conservation Of Energy
Lenz’s law:
Lenz’s law states that the direction emf (or current) is such that it opposes the change in magnetic flux which produces it,
Mathematically the Lenz’s law can be written as

The negative sign represents the effect of Lenz’s law. The magnitude of the induced emf is given by the Faraday’s law. But Lenz’s law gives the direction induced emf.
Lenz’s law is an accordance with the law of conservation of energy.

When the north pole of the magnet is moved towards the coil, the side of the coil facing north pole becomes north as shown in above figure. (Current is produced in the coil and flows in anticlockwise direction).

So work has to be done to move a magnet against this repulsion. This work is converted into electrical energy.

When the north pole of the magnet is moved away from the coil, the end of the coil facing the north pole acquires south polarity. So work has to be done to overcome the attraction. This work is converted into electrical energy. This electrical energy is dissipated as heat produced by the induced current.

Motional Electromotive Force

Consider a rectangular frame MSRN in which the conductor PQ is free to move as shown in figure. The straight conductor PQ is moved towards the left with a constant velocity v perpendicular to a uniform magnetic field B. PQRS forms a closed circuit enclosing an area that change as PQ moves. Let the length RQ = x and RS = I.
The magnetic flux Φ linked with loop PQRS will be BIx.
Since x is changing with time the rate of change of flux Φ will induce an e.m.f. given by

Energy Consideration: A Quantitative Study
Let ‘r’ be the resistance of arm PQ. Consider the resistance of arm QR, RS, and SP as zero. When the arm is moved,
The current produced in the loop,

This current flows through the arm PQ. The arm PQ is placed in a magnetic field. Hence force acting on the arm,

Substituting eq. (1) in eq. (2)

If this arm is pulling with a constant velocity v, the power required for motion P = Fv

The external agent that does this work is mechanical. Where does this mechanical energy go?
This energy is dissipated as heat. The power dissipated by Joule law,

From eq. (3) and (4), we can understand that the workdone to pull the conductor is converted into heat energy in conductor.
Relation between induced charge and magnetic flux:
We know

so the above equation can be written as

We also know magnitude of induced emf

Comparing (1) and (2), we get

Eddy Currents
Whenever the magnetic flux linked with a metal block changes, induced currents are produced. The induced currents flow in a closed paths. Such currents are called eddy currents.
Experiment to Demonstrate Eddy Currents
Experiment -1

Allow a rectangular metal sheet to oscillate in between the pole pieces of strong magnet as shown in figure. When the plate oscillates, the magnetic flux associated with the plate changes. This will induce eddy currents in the plate. Due to this eddy current the rectangular metal sheet comes to rest quickly.
Experiment – 2

Make rectangular slots on the copper plate. These slots will reduce area of plate. Allow this copper plate to oscillate in between magnets. Due to this decrease in area, the eddy current is also decreased. Hence the plate swings more freely.

Some important applications of Eddy Currents:
1. Magnetic braking in trains:
Strong electromagnets are situated above the rails. When the electromagnets are activated, eddy currents induced in the rails. This eddy current will oppose the motion of the train.

2. Electromagnetic damping:
Certain galvanometers have a core of metallic material. When the coil oscillates, the eddy currents are generated in the core. This eddy current opposes the motion and brings the coil to rest quickly.

3. Induction furnace:
Induction furnace can be used to melt metals. A high frequency alternating current is passed through a coil. The metal to be melted is placed in side the coil. The eddy currents generated in the metals produce heat, that melt it.

4. Electric power meters:
The metal disc in the electric power meter (analogue type) rotates due to the eddy currents. This rotation can be used to measure power consumption.

Inductance
An electric current can be induced in a coil by two methods:

1. Mutual induction
2. Self induction

1. Mutual inductance:
Mutual induction:
The phenomenon of production of an opposing e.m.f. in a circuit due to the change in current or magnetic flux linked with a neighboring circuit is called mutual induction.
Explanation

Consider two coils P and S. P is connected to a battery and key. S is connected to a galvanometer. When the key is pressed, a change in magnetic flux is produced in the primary.

This flux is passed through S. So an e.m.f. is produced in the ‘S’. Thus we get a deflection in galvanometer. similarly, when key is opened, the galvanometer shows a deflection in the opposite direction.

Mutual inductance or coefficient of mutual induction:
The flux linked with the secondary coil is directly proportional to the current in the primary
i.e. Φ α I Or Φ = MI
Where M is called coefficient of mutual induction or mutual inductance.
If I = 1, M = Φ
Hence mutual inductance of two coils is numerically equal to the magnetic flux linked with one coil, when unit current flows through the other.

(i) Mutual inductance of two coils:
Expression for mutual inductance:
Consider a solenoid (air core) of cross sectional area A and number of turns per unit length n. Another coil of total number of turns N is closely wound over the first coil. Let I be the current flow through the primary. Flux density of the first coil B= µ₀nI
Flux linked with second coil, Φ = BAN
Φ = µ₀nIAN _____(1)
But we know Φ = MI _______(2)
From eq(1) and eq(2), we get
∴ MI = µ₀nIAN
M = µ₀nAN
If the solenoid is covered over core of relative permeability µ_r
then M = µ_rµ₀nAN

Relation between induced e.m.f. and coefficient of mutual inductance:
Relation between induced e.m.f and mutual inductance
We know induced e.m.f

2. Self inductance:
Self-induction
The phenomenon of production of an induced e.m.f in a circuit when the current through it changes is known as self- induction.
Explanation

Consider a coil connected to a battery and a key. When key is pressed, current is increased from zero to maximum value. This varying current produces a changing magnetic flux around the coil. The coil is situated in this changing flux, so that an e.m.f. is produced in the coil.

This induced e.m.f. is produced in the coil. This induced e.m.f is opposite to applied e.m.f (E). Hence this induced e.m.f is called back e.m.f.

Similarly, when key is released, a back e.m.f is produced which opposes the decay of current in the circuit.

Thus both the growth and decay of currents in a circuit is opposed by the back e.m.f. This phenomenon is called self – induction.

Mathematical expression for self inductance :
Consider a solenoid (air core) of length /, number of turns N and area cross section A. let ‘n’ be the no. of turns per unit length (n = N/l)
The magnetic flux linked with the solenoid,
Φ = BAN
Φ = µ₀nIAN (since B = µ₀nI)
but Φ = LI
∴ LI = µ₀nIAN
L = µ₀nAN
If solenoid contains a core of relative permeability µ_r the L = µ₀µ_rnAN.

Definition of self inductance:
We know NΦ = LI
If I = 1, we get L = NΦ
Self inductance (or) coefficient of self induction may be defined as the flux linked with a coil, when a unit current is flowing through it.
Note: Physically, the self inductance plays the role of inertia.
Relation between induced emf and coefficient of self induction:
When the current through a coil is varied, a back emf produced in the coil. Using Lens law, emf can be written as,

4. Energy stored in an inductor:
When the current in the coil is switched on, a back emf (ε = -Ldt/dt) is produced. This back emf opposes the growth of current. Hence work should be done, against this e.m.f.
Let the current at any instant be ‘I’ and induced emf
E = \(\frac{-\mathrm{d} \phi}{\mathrm{dt}}\)
i.e., work done, dw= EIdt

Hence the total work done (when the current grows from 0 to I₀ is)

This work is stored as potential energy.
V = \(\frac{1}{2}\)LI²

Ac Generator
An ac generator works on electromagnetic induction. AC generator converts mechanical energy into electrical energy.

The structure of an ac generator is shown in the above figure. It consists of a coil. This coil is known as armature coil. This coil is placed in between magnets. As the coil rotates, the magnetic flux through the coil changes. Hence an e.m.f. is induced in the coil.

1. Expression for induced emf:

Take the area of coil as A and magnetic field produced by the magnet as B. Let the coil be rotating about an axis with an angular velocity ω.

Let θ be the angle made by the areal vector with the magnetic field B. The magnetic flux linked with the coil can be written as

Φ = BA cosθ
Φ = BA cosωt [since θ = ωt)
If there are N turns
Φ = NBA cosωt
∴ The induced e.m.f. in the coil,

Let ε₀ = NAB ω,
then s = ε₀ sin ωt.

Expression for current:
When this emf is applied to an external circuit .alternating current is produced. The current at any instant is given by
I = \(\frac{V}{R}\)

(V = ε₀ sin ω)
I = I₀ sin ωt
Where I₀ = ε₀/R, it gives maximum value of current. The direction of current is changed periodically and hence the current is called alternating current.

Variation of AC voltage with time:

Students can Download Chapter 5 Magnetism and Matter Notes, Plus Two Physics Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus Two Physics Notes Chapter 5 Magnetism and Matter

Introduction
The word magnet is derived from the name of an island in Greece called magnesia where magnetic ore deposits were found.
Properties of a magnet

1. When a bar magnet is freely suspended, it points in the north-south direction.
2. There is a repulsive force when north poles (or south poles) are brought close together.
3. We cannot isolate the north or south pole of a magnet.
4. It is possible to make magnets out of iron and its alloys.

Note: The earth behaves as a magnet with the magnetic field pointing approximately from the geographic south to the north.

The Bar Magnet
A magnet has two poles. One pole is North pole and the other South pole.
Magnetic poles:
These two points near the ends of a magnet at which the power of attraction of the magnet is mostly concentrated are called its magnetic poles.
Note: A current carrying solenoid behaves like a bar magnet.

1. The magnetic field lines:
Properties of magnetic field lines

1. The magnetic field lines of a magnet form continuous closed loops.
2. The tangent to the field line at a given point represents the direction of magnetic field at that point.
3. Flux density of magnetic field represents the strength of magnetic field.
4. The magnetic field lines do not intersect

Field lines of bar magnet:

Field lines of current carrying solenoid:

Field lines of electric dipole:

2. Bar magnet as an equivalent solenoid:
Magnetic field along the axis of a solenoid or bar magnet

Consider a solenoid of radius ‘a’ and numberof turns per unit length‘n’. Let 2l be the length and I be the current flowing through the solenoid. Consider a point P at a distance ‘r’ from the centre of solenoid. To find magnetic field at P, we take a circular element of thickness dx at a distance x from the centre of solenoid.
The magnetic field at P due to this small element,

where ndx = N
(total number of turns in a circular element of thickness dx.)
Integrating from x = – l to x = + l, we get

If the point lies at large distance from the solenoid, we can take,
[(r – x)² + a²]^3/2 ≈ r³
r>>a, r>>x
Hence eq.(1) can be written as

Where m is called magnetic moment of the solenoid.

3. The dipole in a uniform magnetic field:
Torque acting on a magnetic dipole:
Consider a magnetic dipole of dipole moment ‘m’ placed in a uniform magnetic field B. If this dipole is rotated to an angle θ, a restoring torque will act on the needle. ie τ = -mBSinθ.
But we know rotational torque τ = la, where I is the moment of inertia of the magnetic dipole and α is the angular acceleration,
lα = -mBSinθ
(Restoring torque and rotational torque are equal in magnitude but opposite in direction)
But α = \(\frac{d^{2} \theta}{d t^{2}}\), for small rotations sinθ ≈ θ.

This equation represents that, the oscillation of this magnetic needle is simple harmonic. When we compare the above equation with standard harmonic.

Potential energy of a magnetic dipole:
The work done in rotating a magnet in a magnetic field is stored in it as its potential energy. If dipole is rotated through an angle (dθ) in a uniform magnetic field B, work done for this rotation,
dw = τdθ
dw = mBsinθdθ
If this magnetic needle is rotated from θ₁ to θ₂, total work done

If dipole is rotated from stable equilibrium (θ₁ = π/2) to θ₂ = 0 we get,
W = -mBcosθ

This work done is stored as magnetic potential energy, ie.

4. The electrostatic analog:
Permanent Magnets And Electromagnets

Substances which retain theirferromagnetic property at room temperature for a longtime, even after the magnetizing field has been removed are called permanent magnets.

The hysteresis curve helps us to select such materials. They should have high retentivity so that the magnet is strong and high coercivity so that the magnetization is not lost by strong magnetic fields. The material should have a wide hysteresis loop. Steel, Alnico, cobalt-steel and nickel are examples.

Electromagnets are usually ferromagnetic materials with low retentivity, low coercivity and high permeability. The hysteresis curve should be narrow so that the energy liberated as heat is small.
The hysteresis curves of both these materials are shown in the above figure.

Magnetism And Gauss’s Law
Gauss’s law in magnetism: The net magnetic flux through any closed surface is zero.

Explanation:

Consider a Gaussian surfaces represented by I and II. Both cases demonstrates that the number of magnetic field lines leaving the surface is balanced by the number of lines entering it. This is true for any closed surface.

The Earth’s Magnetism
Earth’s magnetic field a rise due to electrical currents produced by motion of metallic fluids in the outer core of the earth. This is known as the dynamo effect.

The magnetic field of the earth behaves as magnetic dipole located at the centre of the earth. The axis of the dipole does not coincide with the axis of rotation of the earth. The axis of dipole is titled by 11.3° with axis of rotation of the earth.

The pole near the geographic north pole of the earth is called north magnetic pole (N_m). Likewise, the pole near the geographic south pole is called the south magnetic pole. (S_m).
Note: The north magnetic pole (N_m) behaves like the south pole of a bar magnet (inside the earth). Similarly, the south magnetic pole (S_m) behaves like the north pole of a bar magnet.

(i) Magnetic declination and dip:
The elements of earth’s magnetic field:
The earth’s magnetic field at a place can be completely specified in terms of three quantities. They are

1. Declination
2. Dip
3. Horizontal intensity

Magnetic meridian:
Magnetic meridian at a place is the vertical plane passing through the earth’s magnetic poles.
Geographic meridian:
Geographic meridian at a place is the vertical plane passing through the geographic poles.

1. Magnetic Declination (I):

Declination at a place is the angle between the geographic meridian and magnetic meridian at that place.

2. Dip or Inclination (θ):

The angle between the earth’s magnetic field and the horizontal component of the earth’s magnetic field at a place is called dip. Dip angle changes from place to place. On the equator, the dip is zero and at the poles, the dip is 90°.

3. Horizontal Intensity B_h:
The horizontal intensity at a place is the horizontal components of the earths field.
Relation between Dip, Horizontal intensity and Earth’s magnetic field:

Let B be the Earth’s magnetic field and θ be the angle of dip. Let B_h be the horizontal intensity and Bvthe vertical intensity of the earth’s magnetic field. Then from figure ,we get
B_h = B cos θ
The vertical component, B_v = B sin θ
∴ Tanθ = \(\frac{B_{v}}{B_{h}}\)
and resultant field, B = \(\sqrt{\mathbf{B}_{\mathrm{h}}^{2}+\mathbf{B}_{\mathrm{v}}^{2}}\)

Magnetization And Magnetic Intensity
The magnetic properties of a substance can be studied by defining some parameter such as

1. Intensity of magnetization (M)
2. Magnetic intensity vector (H)
3. Susceptibility
4. Permeability

1. Intensity of magnetisation (M):
It is defined as the magnetic moment per unit volume. It is the measure of the extent to which a specimen is magnetized.

2. Magnetic Intensity Vector (Magnetising field):
It is defined as the magnetic field which produces an induced magnetism in a magnetic substance. If H is the magnetising field and B the induced magnetic field in the material.
ie. H = \(\frac{B}{\mu}\)
where µ is the constant called the magnetic permeability of the medium.

3. Magnetic susceptibility (χ):
Magnetic susceptibility of a specimen is the ratio of its magnetization to the magnetising field,
ie. χ = \(\frac{M}{H}\)

4. Magnetic permeability (µ):
It is the ratio of magnetic field inside a specimen to the magnetising field.
ie. µ = \(\frac{B}{H}\)
µ = µ₀µ_r
µ₀ – Permeability of free space
µ_r – Relative permeability of a medium.

Relation between permeability and susceptibility:
Let a magnetic material be kept in a solenoid. The specimen gets magnetized by induction. The resultant field inside the specimen is the sum of the field due to the current in the solenoid and the field due to the magnetization of the material.
Resultant field B = Field due to current B₀ + Field due to magnetization B_m.
∴ B = B₀ + B_m
But B_m = µ₀M, B₀ = µ₀H
∴ B = µ₀H + µ₀M

Magnetic Properties Of Materials
Materials can be classified as diamagnetic, paramagnetic or ferromagnetic in terms of the susceptibility χ. A material is diamagnetic if χ is negative, para-if χ is positive and small, and Ferro-if χ is large and positive.

1. Diamagnetism:
Diamagnetic substances are those which have tendency to move from stronger to the weaker part of the external magnetic field.
Diamagnetic material in external magnetic field:

Figure shows a bar of diamagnetic material placed in an external magnetic field. The field lines are repelled and the field inside the material is reduced.

Explanation of diamagnetism:
Electrons in an atom orbit around nucleus. These orbiting electrons produce magnetic field. Hence atom possess magnetic moment.

Diamagnetic substances are the ones in which resultant magnetic moment in an atom is zero. When magnetic field is applied, those electrons having orbital magnetic moment in the same direction slow down and those in the opposite direction speed up.

Thus, the substance develops a net magnetic moment in direction opposite to that of the applied field and hence it repels external magnetic field.

Examples:
Some diamagnetic materials are bismuth, copper, lead, silicon, nitrogen (at STP), water and sodium chloride.

Meissner effect:
The phenomenon of perfect diamagnetism in superconductors is called the Meissner effect.

2. Paramagnetism:
Paramagnetic substances are those which get weakly magnetized in an external magnetic field. They get weakly attracted to a magnet.

Reason for paramagnetism:
The atoms of a paramagnetic material possess a permanent magnetic dipole moment. But these magnetic moments are arranged in all directions.

Due to this random arrangement net magnetic moment becomes zero. But in the presence of an external field B₀, the atomic dipole moment can be made to align in the same direction of B0. Hence paramagnetic material shows magnetism in external magnetic field.
Paramagnetic material in external magnetic field:

Figure shows a bar of paramagnetic material placed in an external field. The field lines gets concentrated inside the material, and the field inside is increased.

Examples:
Some paramagnetic materials are aluminium, sodium, calcium, oxygen (at STP) and copper chloride.

Curie law of magnetism:
Curie law of magnetism states that the magnetisation of a paramagnetic material is inversely proportional to the absolute temperature T.

In the case of paramagnetic materials it can be shown that the magnetic susceptibility at temperature is given by

Where C is a constant called curie’s constant.

3. Ferromagnetism:
Ferromagnetic substances are those which gets strongly magnetized in an external magnetic field. They get strongly attracted to a magnet.
Ferro magnetic materials without external magnetic field:

The atoms in a ferromagnetic material possess a dipole moment. These dipoles align in a common direction over a macroscopic volume called domain. Each domain has a net magnetization. Domains are arranged randomly. Hence net magnetic moment of all domains is zero, so ferromagnetic substance does not show magnetism.
Ferro magnetic materials in external magnetic field:

When we apply an external magnetic field B₀, the domains arranged in the direction of B₀ and grow in size. Thus, in a ferromagnetic material the field lines are highly concentrated.

Question 1.
What happens when the external field is removed?
Answer:
In some ferromagnetic materials the magnetisation persists even if external field is removed. Such materials are called hard ferromagnets. Such materials are used to make permanent magnets.
Eg: Alnico
There is a another class of ferromagnetic materials in which the magnetisation disappears on removal of the external field. Such materials are called soft ferromagnetic materials.
Eg: soft iron

Curie temperature:
The ferromagnetic property depends on temperature. At high temperature, a ferromagriet becomes a paramagnet. The domain structure disintegrates with temperature. This disappearance of magnetisation with temperature is gradual. The temperature of transition from ferromagnetic to paramagnetism is called the Curie temperature T_c.

Variation of B and H in paramagnetic materials:
Figure shows the plot of B versus H. As H is gradually increased from zero, B also increase from zero along OP.

As H increases, more and more magnetic dipoles get aligned in the direction of the field. So M increases and hence B increases.

When all the dipoles get aligned in the direction of the field, the curve becomes almost flat. After this there is no increase of B with H.

When H is gradually decreased from P₁ there is no corresponding decrease in the magnetization. The shifting of domains in the ferromagnetic materials is not completely reversible and some magnetization remains even when H is reduced to zero.

The value of the magnetic field when H is zero is called the remanent field Br (Retentivity). If the current in the solenoid is now reversed so that H is in the opposite direction, the magnetic field B can be gradually brought to zero at the point C. The value of H needed to reduce B to zero is called the coercive force He (Coercivity).

The remaining part of curve is obtained by applying H in reverse direction. From these variations it is clear that B always lags behind H. This phenomenon is known as magnetic hysteresis (hysteresis means to lag behind).

The area enclosed by the hysteresis curve gives the loss of energy in the form of heat during the magnetisation – demagnetization cycle.

Permanent Magnets And Electromagnets

Substances which retain theirferromagnetic property at room temperature for a longtime, even after the magnetizing field has been removed are called permanent magnets.

The hysteresis curve helps us to select such materials. They should have high retentivity so that the magnet is strong and high coercivity so that the magnetization is not lost by strong magnetic fields. The material should have a wide hysteresis loop. Steel, Alnico, cobalt-steel and nickel are examples.

Electromagnets are usually ferromagnetic materials with low retentivity, low coercivity and high permeability. The hysteresis curve should be narrow so that the energy liberated as heat is small.
The hysteresis curves of both these materials are shown in the above figure.

Students can Download Chapter 4 Moving Charges and Magnetism Notes, Plus Two Physics Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus Two Physics Notes Chapter 4 Moving Charges and Magnetism

Introduction; Oersted Experiment
The magnetic effect of current was discovered by Danish Physicist Hans Christians Oersted. He noticed that a current in a straight wire makes a deflection in a magnetic needle.

The deflection increases on increasing current. He also found that reversing the direction of current reverses direction of needle. Oersted concluded that current produces a magnetic field around it.

Magnetic Force
1. Sources and fields:
The static charge is the source of electric field. The source of magnetic field is current or moving charge. Both the electric and magnetic fields are vector fields and both obeys superposition principle.

2. Lorentz Force:
The force experienced by moving charge in electric and magnetic field is called Lorentz force. The Lorentz force experienced by charge ‘q’ moving with velocity ‘v’, is given by

= F_electric + F_magnetic
The features of Lorentz Force:

1. The Lorentz force on positive charge is opposite to that on negative charge because it depends on charge ‘q’.
2. The direction of Lorentz force is perpendicular to velocity and magnetic field. Its direction is given by screw rule or right hand rule.
3. Only moving charge experiences magnetic force. For static charge (v = 0), magnetic force is zero.

Note:

1. A charge particle moving parallel or antiparallel to magnetic field will not experience magnetic force and moves undeviated.
2. The work done by magnetic force is zero. Because magnetic force is always perpendicular to direction of velocity.
3. A charged particle entering perpendicular magnetic field (θ = 90°) will make a circular path.
4. The unit of B is Tesla.

3. Magnetic force on current carrying conductor:
Consider a rod of uniform cross section ‘A’ and length ‘e’. Let ‘n’ be the number of electrons per unit volume (number density). ‘v_d’ be the drift velocity of electrons for steady current ‘I’.
Total number of electrons in the entire volume of rod = nAl
Charge of total electrons = nA l.e
‘e’ is the charge of a single electron.
The Lorentz force on electrons,

(I = neAV_d)

Motion In Magnetic Field
Case I:
The charged particle enters perpendicular to magnetic field.(\(\overrightarrow{\mathrm{V}}\) is perpendicular to \(\overrightarrow{\mathrm{B}}\))
When charged particle moves perpendicular to magnetic field, it experiences a magnetic force of magnitude, qVB and the direction of the force is perpendicular to both \(\overrightarrow{\mathrm{B}}\) and \(\overrightarrow{\mathrm{V}}\). This perpendicular magnetic field act as centripetal force and charged particle follows a circular path.

Mathematical explanation:
Let a charge ‘q’ enters into a perpendicular magnetic field B with velocity V. Let r be the radius of circular path. The centripetal force for charged particle is provided by magnetic force.

Thus radius of circle described by charged particle depends on momentum, charge and magnetic field. If ω is the angular frequency
ω = \(\frac{v}{r}\)
Thus from (1) we get

The frequency ν = \(\frac{q B}{2 \pi m}\)
Thus frequency of revolution of charge is independent of velocity (and hence energy)
The time period T = \(\frac{2 \pi \mathrm{m}}{\mathrm{qB}}\)
(ν = \(\frac{1}{T}\)).

Case II:
The charged particles enters at an angle ‘θ’ with magnetic field.
Since the charged particle enters at an angle ‘θ’ with magnetic field, its velocity will have two components; a component parallel to magnetic field, V_॥ (Vcosθ) and a component perpendicular to the magnetic field, V_⊥(Vsinθ).

The parallel component of velocity remains unaffected by magnetic field and it causes charged particle to move along the field.

The perpendicular component makes the particle to move in circular path. The effect of linear and circular movement produce helical motion.

Pitch and Helix: The distance moved along magnetic field in one rotation is called pitch ‘P’

The radius of circular path of motion is called helix.

Motion In Combined Electric And Magnetic Fields
1. Velocity selector:
A transverse electric and mag¬netic field act as velocity selector. By adjusting value of E and B, it is possible to select charges of particular velocity out of a beam containing charges of different speed.

Explanation:
Consider two mutually perpendicular electric and magnetic fields in a region. A charged particle moving in this region, will experience electric and magnetic force. If net force on charge is zero, then it will move undeflected. The mathematical condition for this undeviation is

The charges with this velocity pass undeflected through the region of crossed fields.

2. Cyclotron
Uses: It is a device used to accelerate particles to high energy.
Principles: Cyclotron is based on two facts

1. An electric field can accelerate a charged particle.
2. A perpendicular magnetic field gives the ion a circular path.

Constructional Details:
Cyclotron consists of two semicircular dees D₁ and D₂, enclosed in a chamber C. This chamber is placed in between two magnets. An alternating voltage is applied in between D₁ and D₂. An ion is kept in a vacuum chamber.

Working:
At certain instant, let D₁ be positive and D₂ be negative. Ion (+ve) will be accelerated towards D₂ and describes a semicircular path (inside it). When the particle reaches the gap, D₁ becomes negative and D₂ becomes positive. So ion is accelerated towards D₁ and undergoes a circular motion with larger radius. This process repeats again and again.

Thus ion comes near the edge of the dee with high K.E. This ion can be directed towards the target by a deflecting plate.

Mathematical expression:
Let V be the velocity of ion, q the charge of the ion and B the magnetic flux density. If the ion moves along a semicircular path of radius ‘r’, then we can write

[Since θ =90°, B is perpendicular to v]
or v = \(\frac{q B r}{m}\) _____(1)
Time taken by the ion to complete a semicircular path.

Eq. (2) shows that time is independent of radius and velocity.

Resonance frequency (cyclotron frequency):
The condition for resonance is half the period of the accelerating potential of the oscillator should be ‘t’. (i.e.,T/2 = t or T = 2t). Hence period of AC
T = 2t

K.E of positive ion

Thus the kinetic energy that can be gained depends on mass of particle charge of particle, magnetic field and radius of cyclotron.
Limitations:

1. As the particle gains extremely high velocit, the mass of particle will be changed from its constant value. This will affect the normal working of cyclotron as frequency depends of mass of particle.
2. Very small particles like electron can not be accelerated using cyclotron. This is because as the mass of electron is very small the cyclotron frequency required becomes extremely high which is practically difficult.
3. Neutron can’t be accelerated

Magnetic Field Due To Current Element; Biot Savart Law

The magnetic field at any point due to an element of current carrying conductor is

1. Directly proportional to the strength of the current (I)
2. Directly proportional to the length of the element (dl)
3. Directly proportional to the sine of the angle (θ) between the element and the line joining the midpoint of the element to the point.
4. Inversely proportional to the square of the distance of the point from the element

The direction of magnetic field is perpendicularto the plane containing d/and rand is given by right hand screw rule.
In the above expression \(\frac{\mu_{0}}{4 \pi}\) is the constant of proportionality and µ₀ is called the permeability of vacuum. Its value is 4π × 10^-7 TmA^-1.
Note: A magnetic field acting perpendicularly in to the plane of the paper is represented by the symbol ⊗ and a magnetic field acting perpendicularly out of the paper is represented by the symbol ⵙ.

Comparison between Biot-Savart Law and Coulomb’s law
Similarities:

1. The two laws are based on inverse square of distance and hence they are long range.
2. Both electrostatic and magnetic fields obey superposition principle.
3. The source of magnetic field is linear; (the current element \(\overrightarrow{\mathrm{ldl}}\)). The source of electrostatic force is also linear; (the electric charge).

Differences:

Magnetic Field On The Axis Of A Circular Current Loop

Consider a circular loop of radius ‘a’ and carrying current ‘I’. Let P be a point on the axis of the coil, at distance x from A and r from ‘O’. Consider a small length dl at A. The magnetic field at ‘p’ due to this small element dl,

\(\mathrm{dB}=\frac{\mu_{0} \mathrm{Idl}}{4 \pi \mathrm{x}^{2}}\) _____(1)
[since sin 90° – 1]
The dB can be resolved into dB cosΦ (along Py) and dB sinΦ (along Px).
Similarly consider a small element at B, which produces a magnetic field ‘dB’ at P. If we resolve this magnetic field we get.
dB sinΦ (along px) and dB cosΦ (along py¹)
dB cosΦ components cancel each other, because they are in opposite direction. So only dB sinΦ components are found at P, so total filed at P is

but from ∆AOP we get, sinΦ = a/x
∴ We get

Point at the centre of the loop: When the point is at the centre of the loop, (r = 0)
Then,

1. Magnetic field at the centre of loop:
The magnetic field at a distance x from centre of loop is given by

The direction of magnetic field due to current carrying circular loop is given by right hand thumb rule.

Thumb Rule: Curl of palm of right hand around circular coil with fingers pointing in the direction of current. Then extended thumb gives the direction of magnetic field.

Note:

1. An anticlockwise current gives a magnetic field out of the coil and a clockwise current gives a magnetic field into the coil.
2. The current carrying loop is equivalent to magnetic dipole of dipole moment m = IA

Ampere’s Circuital Law
According to ampere’s law the line integral of magnetic field along any closed path is equal to µ₀ times the current passing through the surface.

Applications Of Ampere’s Circuital Law
1. Long straight conductor:
Consider a long straight conductor carrying T ampere current. To find magnetic field at ‘P’, we construct a circle of radius r (passing through P).

According to Ampere’s circuital law we can write

[B and dl are parallel]
B∫dl = µ₀I
B2πr = µ₀I
B = \(\frac{\mu_{0} I}{2 \pi r}\)

2. Magnetic field due to long solenoid:

Consider a solenoid having radius T. Let ‘n’ be the number of turns per unit length and I be the current flowing through it.
In order to find the magnetic field (inside the solenoid) consider an Amperian loop PQRS. Let V ‘ be the length and ‘b’ the breadth
Applying Amperes law, we can write

Substituting the above values in eq (1),we get
Bl = µ₀ l_enc ____(2).
But l_enc = n l I
where ‘nl ’ is the total number of turns that carries current I (inside the loop PQRS)
∴ eq (2) can be written as
Bl = µ₀ nIl
B = µ₀nI
If core of solenoid is filled with a medium of relative permittivity µ_r. then
B = µ₀µ_rnl

3. The toroid:
Consider a toroid of average radius ‘r’. Let ‘n’ be the number of turns per unit length. Let I be the current flowing through the toroid. In order to find magnetic field inside the toroid, an camperian loop of radius ‘r’ is considered.

Applying Amperes law to the loop, we can write

Where ‘n2πr ‘ is the total number of turns of the solenoid that carries current I (inside the Amperian loop) Integrating the eq(1) we get
B 2πr = µ₀2πrI
B = µ₀n I
If the core of the solenoid is filled with a medium of relative permeability µ_r then the above equation is modified as

Note: The magnetic field due to toroid is same as that due to solenoid.

Force Between Two Parallel Currents, The Ampere Force Between Two Parallel Conductors

P and Q are two infinitely long conductors placed parallel to each other and separated by a distance r, Let the current through P and Q be l₁ and l₂ respectively.
Magnetic field at a distance ‘r’ from P is

Conductor ‘Q’ is placed in this magnetic field.
If l₂ is the length of the conductor ‘Q’, the Lorentz force on ‘Q’ is

∴ Force per unit length can be written as,

Where f = \(\frac{F}{\ell_{2}}\)
Note:

1. When currents are in the same direction, the force is attractive
2. If the currents are in the opposite direction, the force is repulsive.

Definition of ampere:
An ampere is defined as that constant current which if maintained in two straight parallel conductors of infinite lengths placed one meter apart in vacuum will produce between a force of 2 × 10^-7 Newton per meter length.

Force On A Current Loop, Magnetic Dipole
1. Torque on a rectangular current loop in uniform magnetic filed:

Considers rectangular coil PQRS of N turns which is suspended in a magnetic field, so that it can rotate (about yy 1). Let ‘l’ be the length (PQ) and ‘b’ be the breadth (QR).

When a current l flows in the coil, each side produces a force. The forces on the QR and PS will not produce torque. But the forces on PQ and RS will produce a Torque.
Which can be written as
τ = Force × ⊥ distance _______(1)
But, force = BlI ______(2)
[since θ = 90° ]
And from ∆QTR , we get
⊥ distance (QT) = b sin θ ______(3)
Substituting the vales of eq (2) and eq (3) in eq(1) we get
τ = BIl b sin θ
= BIA sin θ [since lb = A (area)]
τ = IAB sin θ
τ = mB sin θ [since m = IA]

If there are N turns in the coil, then
τ = NIAB sin θ

2. Circular Current loop as a magnetic di pole:
Current loop of any shape act as magnetic dipole.
Current loop acts as magnetic dipole:
The magnetic field due to circular loop of radius R carrying current I at a distance ‘x’ from the centre of loop (on the axis of loop) is given by,

The magnetic field at large distance (x>>R) on axis of loop is

Dividing and multiplying by π

Comparison of magnetic dipole and electric dipole:
The equation (1) is similar to electric field due to electric dipole at a distance ‘x’ from the centre of dipole on its axial line.

Comparing eq(1) and (2), we get 1

m → P
B → E
From this comparison it is clear that a circular current loop acts as a magnetic dipole.

3. The magnetic dipole moment of a revolving electron:
According to Bohr’s model of atom, electrons are revolving around nucleus in its orbit. The electron revolving in its orbit can be considered as circular current loop.

Consider an electron of charge e, revolving around nucleus of charge +ze as shown in figure. The uniform, circular motion of electron constitute current ‘I’. If T is the period of revolution e
I = \(\frac{e}{T}\) _____(1)
If r is the radius of orbit and V s the orbital speed then
T = \(\frac{2 \pi r}{v}\)
Substituting this in (1), we get
I = \(\frac{e v}{2 \pi r}\)
The magnetic moment associated orbiting electron is denoted by µ₁

A = πr², area of orbit
Dividing and multiplying by m_e (Mass of electron)

Applying Quantum Theory, Bohr has proposed that angular momentum of electron can take only discrete values given by,
l = \(\frac{\mathrm{nh}}{2 \pi}\) (Bohr’s quantization condition where n = 1, 2, 3, ……..etc) where h is Plank’s constant. Thus

The orbital magnetic moment of electron is given by

Bohr Magneton: We get the minimum value of magnetic moment, when n = 1 ie

(when n = 1)
Its value is 9.27 × 10^-24 Am². This is called Bohr magneton.
Gyromagnetic Ratio:
The orbital magnetic moment of electron is related to orbital angular momentum ‘l’ as

The ratio of orbital magnetic moment to orbital angular momentum is constant. This constant is called gyromagnetic ratio. Its value is 8.8 × 10¹⁰ c/kg for an electron.

The Moving Coil Galvanometer
It is an instrument used to measure small current.
Principle: A conductor carrying current when placed in a magnetic field experiences a force, (given by Fleming’s left hand rule).
Construction:

A moving coil galvanometer consists of rectangular coil of wire having area ‘A’ and number of turns ‘n’ which is wound on metallic frame and is placed between two magnets. The magnets are concave in shape, which produces radial field.

Working: Let ‘l’ be the current flowing the coil, Then the torque acting on the coil.
τ = NIAB Where A is the area of coil and B is the magnetic field.
This torque produces a rotation on coil, thus fiber is twisted and angle (Φ). Due to this twisting a restoring torque (τ = KΦ) is produced in spring.
Under equilibrium, we can write
Torque on the coil = restoring torque on the spring
or NIAB = kΦ
or Φ = (\(\frac{\mathrm{BAN}}{\mathrm{K}}\))I
The quantity inside the bracket is constant for a galvanometer.
Φ α I
The above equation shows that the deflection depends on current passing through galvanometer.

1. Ammeter and voltmeter:
For measuring large current, the galvanometer can be converted in to ammeter and voltmeter.
Ammeter:
Ammeter is an instrument used to measure current in the circuit.

A galvanometer can be converted into an ammeter by a low resistance (shunt) connected parallel to it.

Theory:
Let G be the resistance of the galvanometer, giving full deflection fora current Ig.

To convert it into an ammeter, a suitable shunt resistance ‘S’ is connected in parallel. In this arrangement Ig current flows through Galvanometer and remaining (I – Ig) current flows through shunt resistance.
Since G and S are parallel
P.d Across G = p.d across
Ig × G = (I – Ig)S

Connecting this shunt resistance across galvanometer we can convert a galvanometer into ammeter.

2. Conversion of galvanometer into voltmeter:
To convert a galvanometer into a voltmeter, a high resistance is connected in series with it.

Theory:
Let Ig be the current flowing through the galvanometer of resistance G. Let R be the high resistance co connected in series with G.

From figure we can write
V = IgR + IgG
V – IgG = IgR

Using this resistance we can covert galvanometer in to voltmeter.

Current sensitivity:
The current sensitivity of galvanometer is the deflection produced by unit current.

The current sensitivity can be increased by increasing number of turns.

The voltage sensitivity:
The voltage sensitivity of galvanometeris the deflection produced by unit voltage.

The increase in number of turns will not change voltage sensitivity.
When number of turns double (N → 2N), the resistance of the wire will be double (ie. R → 2R). Hence the voltage sensitivity does not change.

Students can Download Chapter 8 The d and f Block Elements Notes, Plus Two Chemistry Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus Two Chemistry Notes Chapter 8 The d and f Block Elements

The d-block (Transition elements) – elements of the groups 3 – 12 in which the d-orbitals are progressively filled. The f-block (Inner transition elements) – elements in which the 4f and 5f orbitals are progressively filled.

The Transition Elements (d-block):
Their position is in between more electropositive s-block and more electronegative p-block elements.

General Electronic Configuration:
(n -1) d^1-10ns^1-2
The transition metals are classified as,

1. 3d series – 1^st transition series (Sc – Zn)
2. 4d series – 2^nd transition series (Y – Cd)
3. 5d series – 3^rd transition series (La, Hg – Hg)
4. 6d series – 4^th transition series (Ac, Rf – Cn)

Pseudo transition elements – Zn, Cd and Hg are not regarded as transition elements because their orbitals are completely filled in the ground state as well as in their common oxidation states, [(n – 1)d¹⁰ns²]. But they included in transition series due to some similarity to transition metals.

General Properties of Transition Elements:
1. Physical Properties:
High tensile strength, ductility malleability, high thermal and electrical conductivity and metallic lustre, very much hard and low volatile (except Zn, Cd and Hg), high mp (due to interatomic metallic bonding) and bp.

2. Variation in Atomic and Ionic Sizes:
Decreases with increasing atomic number because the new electron enters a d-orbital with low shielding power.

3. Ionisation Enthalpies:
Due to an increase in nuclear charge which accompanies the filling of the inner d-orbitals, there is an increase in ionisation enthalpy along the series.

First ionisation potential/enthalpy of the 5d series are higher than those of the 3d and 4d metals. This is due to lanthanoid contraction caused by poor shielding of the 4f electrons.

4. Oxidation State:
Transition elements shows various oxidation states which aries due to incomplete filling of d-orbital. The elements which give the greatest number of oxidation state occur in or near the middle of the series, e.g. Mn (+2 to +7)

5. Trends in the M²⁺/M Standard Electrode Potential:
The general trend towards less negative E° values across the series is related to the general increase in the sum of the first and second ionisation enthalpies.

6. Trends in Stability of Higher Oxidation State:
In halides, the ability of fluorine to stabilise the highest oxdn. state is due to either higher lattice energy or higher bond enthalpy. The stability of Cu²⁺(aq) rather than Cu⁺(aq) is due to the much more negative Δ_hydH° of Cu²⁺(aq) than Cu⁺(aq).

7. Chemical Reactivity:
Many of them are sufficiently electropositive to dissolve in mineral acids, a few are unaffected by simple acids. The metals of the first series are relatively more reactive and are oxidised by 1M H⁺ (except Cu).

8. Magnetic Properties:
(a) Diamagnetism:
Due to paired electrons, they are weakly repelled by applied magnetic field.

(b) Paramagnetism:
Due to presence of unpaired electrons paramagnetic substances are weakely attracted by applied magnetic field.

(c) Ferromagnetic:
Extreme form of paramagnetism, very strongly attracted by magnetic field. For transition elements, the magnetic moment is determined by the number of unpaired electrons and is calculated by spin-only formula,
\(\mu=\sqrt{n(n+2)}\)
where n is the number of unpaired electrons. The unit is Bohr magneton (BM). e.g.

9. Formation of Coloured Ions:
Most of the transition metal ions are coloured due to d-d transition of electrons. When an electron from a lower energy d orbital is excited to a higher energy d orbital, the energy of excitation corresponds to the frequency of light absorbed. The colour observed corresponds to the complementary colour of the light absorbed,

Example:

1. 1. • Sc³⁺(3d°), Ti⁴⁺ (3d°), Zn²⁺ (3d¹⁰) – Colourless
      • Ti³⁺ (3d¹) – Purple
      • Mn²⁺ (3d⁵) – Pink
      • Fe²⁺ (3d⁶) – Yellow
      • Fe³⁺ (3d⁵) – Green.

10. Formation of Complex Compounds:
They can form a large number of complex compounds due to the comparatively smaller sizes of the metal ions, their high ionic changes and the availability of d- orbital for bond formation.

(a) Catalytic Properties:
It is due to their ability to adopt multiple oxidation states and to form complexes, eg: V₂O₅ (Contact process), Fe (Haber’s process), Ni/Pt/Pd (Hydrogenation of hydrocarbon), TiCl₄ & Al(C₂H₅)₃ (Zeigler – Natta catalyst – polymerisation of ethene and propene).

11. Formation of Interstitial Compounds:
They are formed when small atoms like H, C or N are trapped inside the crystal lattices of metals. They hey are non-stoichiometric and are neither ionic nor covalent.

Characteristics – high m.p, very hard, retain metallic conductivity, chemically inert.

12. Alloy Formation:
Due to similar radii, they form alloys very easily.

Some Important Compounds of Transition Elements:
(a) Potassium Dichromate (K₂Cr₂O₇):
Obtained by the fusion of chromite ore (K₂Cr₂O₄ with Na/K₂CO₃ in pressure of air.

4FeCr₂O₄ + 8Na₂CO₃ + 7O₂ → 8Na₂CrO₄ + 2Fe₂O₃ + 8CO₂

The yellow solution of sodium chromate is filtered and acidified with H₂SO₄ to give orange sodium di chromate.

2Na₂CrO₄ + 2H⁺ → Na₂Cr₂O₇ + H₂O
Na₂Cr₂O₇ is converted into K₂Cr₂O₇ by adding KCl.
Na₂Cr₂O₇ + 2KCl → K₂Cr₂O₇ + 2NaCl

The chromate and dichromate are interconvertible in aqueous solution depending upon P^H of the solution.
2CrO₄^2- + 2H⁺ → Cr₂O₂^2- + H₂O
CrO₇^2- + 2OH^– → 2CrO₄^2- + H₂O

Uses:
K₂/Na₂Cr₂O₇-strong oxidising agents. Na₂Cr₂O₇ used in organic chemistry due to its greater solubility. K₂Cr₂O₇ is used as primary standard in volumetric analysis. Oxidising action in acidic.
solution:
Cr₂O₂^2- + 14H⁺ + 6e^– → 2Cr³⁺ + 7H₂O
e.g. It oxidises l^– to l₂, S^2- to S, Sn²⁺ to Sn⁴⁺ and Fe²⁺ to Fe³⁺

(b) Pottassium Permanganate (KMnO₄):
Preparation:
By the fusion of pyrolusite ore (MnO₂) with KOH and oxidising agent like KNO₃to give dark green K₂MnO₄ which disproportionates in a neutral or acidic solution to give KMnO₄.

2MnO₂ + 4KOH + O₂ → 2K₂MnO₄ + 2H₂O
3MnO₄^2- + 4H⁺ → 2MnO₄^– + MnO₂ + H₂O

Commercial preparation:
By the electrolytic oxidation of MnO₄^2- ion (Manganate ion).

Laboratory preparation:
By oxidising Mn²⁺ salt using peroxodisulphate.
2Mn²⁺ + 5S₂O₈^2- + 8H₂O → 2MnO₄^– + 10SO₄^2- + 16H^–

Properties:
Dark purple colour, isostructural with KClO₄, on heating decomposes at 513 K
(2KMnO₄ → K₂MnO₄ + MnO₂ + O₂).
It has temperature dependent paramagnetism. Manganate ion – green, paramagnetic (one unpaired electron). Permanganate ion – purple, diamagnetic. The manganate and permanganate ions are tetrahedral.

Acidified permanganate solution oxidises oxalates to CO₂, Fe²⁺ to Fe³⁺, NO₂^– to N03^–, I^– to I₂, S^2- to S, SO₃^2- to SO₄^2-.

Uses:
In analytical chemistry; in organic chemistry as oxidising agent; for bleaching wool, cotton, silk and other textile fibres; fordecolourisation of oils.

The Inner Transition Elements (f-block):
It consist of the two series, lanthanoids (the 14 elements following La) and actinoids (the 14 elements following Ac).

The Lanthanoids:
1. General Electronic Configuration:
(n – 2) f^1-14(n-1)d^0-1ns²

2. Atomic and Ionic Sizes:
There is a regular (steady) decrease in the size of atoms/ions with increase in atomic number as we move across from La to Lu. This slow decrease in size is known as lanthanoid contraction.

(a) Cause of Lanthanoid Contraction:
The 4f electrones constitute inner shells and are ineffective in screening the nuclear charge. Consequently, the attraction of the nucleus for the electrones in the outer most shell increases with increase in atomic number and the electron cloud shrinks. As a result, the size of the lanthanoids decreases.

Consequences:
(a) Similarity of second and third transition series:
The atomic radii of 2^nd row transition series are almost similar to those of third row transition series. Zrand Hf have almost similar radii. This makes it difficult to separate the elements in the pure state.

(b) Variation in the basic strength of hydroxides:
The size of M³⁺ ion decreases and covalent character M-OH increases. OH^– ions are not easily released. Hence the basic strength of oxides and hydroxides decrease from lanthanum to lutetium.

3. Oxidation States:
They display variable oxidation state. The most stable oxidaiton state is +3. They also show +2 and +4 oxidaiton states.

4. General Characteristics:
Due to f-f transition, they form coloured ions. They form carbides when heated with carbon, liberates H₂ from dilute acids, form halides, oxides and hydroxides, form alloys, e.g. Misch metal.

Actinoids:
14 elements from Th to Lr, radio active, most of the elements are man made.

1. Electronic configuration-similar to Lanthanoids, but the last electron is filled in 5f – orbital.

2. Ionic Sizes:
The gradual decrease in the size of the atoms or ions across the series (actinoid contraction). It is greater because of poor shielding by 5f electrons.

3. Oxidation States:
Common +3 oxidation state, also show +4, +5, +6, +7. But +3 and +4 ions tend to hydrolyse.

4. General Characteristics and Comparison with Lanthanoids:
Highly reactive metals. HCl acid attacks all metals, alkalies have no action, magnetic properties are more complex than those of lanthanoids.

Application of d- and f-block Elements:
Iron and steels-most important construction materials, TiO- used in pigment industry, MnO₂ – used in dry battery cells. Battery industry also requires Zn and Ni/Cd. Cu, Ag and Au – coinage metals.

Metals and metal compounds – essential catalysts.
PdCl₂ – used in Wacker Process
AgBr -used in photography.

Students can Download Chapter 3 Current Electricity Notes, Plus Two Physics Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus Two Physics Notes Chapter 3 Current Electricity

Introduction
In the present chapter, we shall study some of the basic laws concerning steady electric currents.

Electric Current
Rate of flow of electric charge is called electric current. or

Electric Currents In Conductors

• Conductors: Free electrons are found in conductors. The electric current in conductors is due to the flow of electrons.
• Electrolytes: The current in electrolyte is due to flow of ions.
• Semiconductor: The current in semiconductor is due to flow of both holes and electrons.

Ohm’s Law
At constant temperature, the current through a conductor is directly proportional to the potential difference between its ends.
V α I (or)

where R is constant, called resistance of materials.

1. Resistance of a material:
Factors Affecting Resistance of Resistor:
For a given material resistance is directly proportional to the length and inversely proportional to the area of cross-section.
R ∝ \(\frac{\mathrm{L}}{\mathrm{A}}\)

where ρ is the constant of proportionality and is called resistivity of material.

Resistivity (coefficient of specific resistance) of a Material:
The resistance per unit length for unit area of cross-section will be a constant and this constant is known as the resistivity of the material. The resistivity or coefficient of specific resistance is defined as the resistance offered by a resistor of unit length and unit area of cross-section.

Resistivity is a scalar quantity and its unit is Ω-m.

Conductance and conductivity:
The reciprocal of resistance is called conductance and the reciprocal of resistivity is called conductivity. The SI unit of conductance is seimen and that for conductivity is seimen per meter. The unit of conductance can also be expressed as Ω^-1.

Current density: Current per unit area is called current density
current density j = \(\frac{I}{A}\)
Vector form

Mathematical expression of Ohm’s law in terms of j and E:
Considers conductor of length i. Let V’ be the potential difference between the two ends of a conductor.
According to ohms law
We know V= IR

This potential difference produces an electric field E in the conductor. The p.d. across the conductor also can be written as
V = El _____(2)
Comparing (1) and (2), we get
El = jρl
E = jρ
The above relation can be written in vector form as

where σ is called conductivity of the material.

Drift Of Electrons And The Origin Of Resistivity
Random thermal motion of electrons in a metal:
Every metal has a large number of free electrons. Which are in a state of random motion within the conductor. The average thermal speed of the free electrons in random motion is of the order of 10⁵m/s.

Does random thermal motion produce any current? The directions of thermal motion are so randomly distributed. Hence the average thermal velocity of the electrons is zero. Hence current due to thermal motion is zero.

(a) Drift Velocity (vd):
The average velocity acquired by an electron under the applied electric field is called drift velocity.

Explanation: When a voltage is applied across a conductor, an electric filed is developed. Due to this electric field electrons are accelerated. But while moving they collide with atoms, lose their energy and are slowed down. This acceleration and collision are repeated through the motion. Hence electrons move with a constant average velocity. This constant average velocity is called drift velocity.

(b) Relaxation time (τ):
Relaxation time is the average of the time between two successive collisions of the free electrons with atoms.

(c) Expression for drift velocity:
Let V be the potential difference across the ends of a conductor. This potential difference makes an electric field E. Under the influence of electric field E, each free electron experiences a Coulomb force.
F = -eE
or ma = -eE
a = \(\frac{-e E}{m}\) _____(1)
Due to this acceleration, the free electron acquires an additional velocity. A metal contains a large number of electrons.
For first electron, additional velocity acquired in a time τ,
v₁ = u₁ + aτ₁
where u₁ is the thermal velocity and τ is the relaxation time.
Similarly the net velocity of second, third,……electron

v₂ = u₂ + aτ₂
v₃ = u₃ + aτ₃
v_n = u_n + aτ_n
∴ Average velocity of all the ‘n’ electrons will be

V_av = 0 + aτ (∴ average thermal velocity of electron is zero)
where τ = \(\frac{\tau_{1}+\tau_{2}+\ldots \ldots \ldots+\tau_{n}}{n}\)
where V_av is the average velocity of electron under an external field. This average velocity is called drift velocity.
ie. drift velocity V_d = aτ _____(2)

(d) Relation between electric current and drift speed:
Consider a conductor of cross-sectional area A. Let n be the number of electrons per unit volume. When a voltage is applied across a conductor, an electric filed is developed. Let v_d be the drift velocity of electron due to this field.
Total volume passed in unit time = Av_d
Total number of electrons in this volume = Av_dn
Total charge flowing in unit time=Av_dne
But charge flowing per unit time is called current I ie. current, I = Av_dne
I = neAv_d
Now current density J can be written as
J = nev_d (J= I/A)
Deduction of Ohm’s law: (Vector form)
We know current density
J = nv_de

1. Mobility: Mobility is defined as the magnitude of the drift velocity per unit electric field.

Limitations Of Ohm’s Law
Certajn materials do not obey Ohm’s law. The deviations of Ohm’s law are of the following types.
1. V stops to be proportional to I.

Metal shows this type behavior. When current through metal becomes large, more heat is produced. Hence resistance of metal increases. Due to increase in resistance the V-I graph becomes nonlinear. This nonlinear variation is shown by solid line in the above graph.

2. Diode shows this type behavior. We get different values of current for same negative and positive voltages.

3. This type behavior is shown by materials like GaAs. there is more than one value of V for the same current I.

Note: The materials which donot obey ohms law are mainly used in electronics.

Resistivity Of Various Materials
The materials are classified as conductors, semi conductors, and insulators according to their resistivities. Commercially produced resistors are of two types.

1. Wire bound resistors
2. Carbon resistors

1. Wire bound resistor:
Wire wound resistors are made by winding the wires of an alloy.
Eg: Manganin, Constantan, Nichrome.

2. Carbon resistors:
Resistors in the higher range are made mostly from carbon. Carbon resistors are compact. Carbon resistors are small in size. Hence their values are given using a colourcode.

(i) Colourcode of resistors:
The resistance value of commercially available resistors are usually indicated by certain standard colour coding.

The resistors have a set of coloured rings on it. Their significance is indicated in the table The first two bands from the end indicated the first two significant digits and the third band indicates the decimal multiplier. The last metallic band indicates the tolerance.
Value of colours:

Illustration:

The colour code indicated in the given sample is Red, Red, Red with a silver ring at the right end. Then the value of given resistance is 22 × 10² ±10%.

Temperature Dependence Of Resistivity:
The resistivity of a material is found to be dependent on the temperature. The resistivity of a metallic conductor is approximately given by,
ρ_T = ρ_o[1 + α(T – T_o)]
where ρ_T is the resistivity at a temperature T and ρ_o is the resistivity at temperature T_o. α is called the temperature coefficient of resistivity.
Variation of resistivity in metals:

The temperature coefficient (α) of metal is positive. Which means resistivity of metal increases with temperature. The variation of resistivity of copper is as shown in above figure.
Eg: Silver, copper, nichrome, etc.
Variation of resistivity in semi conductor:

The temperature coefficient (α)of semiconductor is negative. Which means that resistivity decreases with increase in temperature. The variation of resistivity with temperature for a semiconductor is shown in above figure.
Eg: Carbon,Germanium,silicon
Variation of resistivity in standard resistors:

standard resistors, the variation of resistivity will be very little with temperatures. The variation of resistivity with temperature for standard resistors is show above.
Eg: Manganin and constantan.
Explanation for the variation of resistivity:
The resistivity of a material is given by

The above equation shows that, resistivity depends inversely on number density and relaxation time τ.
Metals:
Number density in metal does not change with temperature. But average speed of electrons increases. Hence frequency of collision increases. The increase in frequency of collision decreases the relaxation time τ. Hence the resistivity of metal increases with temperature.

Insulators and semiconductors:
For insulators and semiconductors, the number density n increases with temperature. Hence resistivity decreases with temperature.

Electrical Energy, Power

Consider two points A and B in a conductor. Let V_A and V_B be the potentials at A and B respectively. The potential At A is greater than that B and difference in potential is V.

If ∆Q charge flows from A to B in time ∆t. The potential energy of charge will be decreased. The decrease in potential energy due to charge flow from A to B,
= V_A∆Q – V_B∆Q
= (V_A – V_B)∆Q
= V∆Q (V_A – V_B = V)
This decrease in PE appeared as KE of flowing charges. But we know, the kinetic energy of charge carriers do not increase due to the collisions with atoms. During collisions, the kinetic energy gained by the charge carriers is shared with the atoms.

Hence the atoms vibrate more vigorously ie. The conductor heats up. According to conservation of energy, heat developed in between A and B in time ∆t
∆H = decrease in potential energy
∆H = V∆Q
∆H = VI∆t (∵ ∆Q=I∆t)
\(\frac{\Delta \mathrm{H}}{\Delta \mathrm{t}}\) = VI
Rate of workdone is power, ie

using Ohm’s law V = IR

It is this power which heats up the conductor.
Power transmission:
The electric power from the electric power station is transmitted with high voltage. When voltage increases, the current decreases. Hence heat loss decreases very much.

Combination Of Resistors – Series And Parallel Combination
Resistors in series:
Consider three resistors R₁, R₂ and R₃ connected in series and a pd of V is applied across it.

In the circuit shown above the rate of flow of charge through each resistor will be same i.e. in series combination current through each resistor will be the same. However, the pd across each resistor are different and can be obtained using ohms law.
pd across the first resistor V₁ = I R₁
pd across the second resistor V₂, = I R₂
pd across the third resistor V₃ = I R₃
If V is the effective potential drop and R is the effective resistance then effective pd across the combination is V = IR
Total pd across the combination = the sum pd across each resistor, V = V₁ + V₂ + V₃
Substituting the values of pds we get IR = IR₁ + IR₂ + IR₃
Eliminating I from all the terms on both sides we get

Thus the effective resistance of series combination of a number of resistors is equal to the sum of resistances of individual resistors.

1. Resistors in parallel:
Consider three resistors R₁, R₂ and R₃ connected in parallel across a pd of V volt. Since all the resistors are connected across same terminals, pd across all the resistors are equal.

As the value of resistors are different current will be different in each resistor and is given by Ohm’s law
Current through the first resistor
I₁ = \(\frac{V}{R_{1}}\)
Current through the second resistor
I₂ = \(\frac{V}{R_{2}}\)
Current through the third resistor
I₃ = \(\frac{V}{R_{3}}\)
Total current through the combination is
I = \(\frac{V}{R}\), where R is the effective resistance of parallel combination.
Total current through the combination = the sum of current through each resistor
I = I₁ + I₂ + I₃
Substituting the values of current we get

Eliminating V from all terms on both sides of the equations, we get

Thus in parallel combination reciprocal of the effective resistance is equal to the sum of reciprocal of individual resistances. The effective resistance in a parallel combination will be smaller than the value of smallest resistance.

Cells, Emf, Internal Resistance
Electrolytic cell:
Electrolytic cell is a simple device to maintain a steady current in an electric circuit. A cell has two electrodes. They are immersed in an electrolytic solution.

E.M.F:
E.M.F. is the potential difference between the positive and negative electrodes in an open circuit. ie. when no current is flowing through the cell.

Voltage:
Voltage is the potential difference between the positive and negative electrodes, when current is flowing through it.

Internal resistance of cell:
Electrolyte offers a finite resistance to the current flow. This resistance is called internal resistance (r).

Relation between ε, V and internal drop:
Consider a circuit in which cell of emfs is connected to resistance R. Let r be the internal resistance and I be the current following the circuit.

According to ohms law,
current flowing through the circuit

V is the voltage across the resistor called terminal voltage. Ir is potential difference across internal resistance called internal drop.

Cells In Series And Parallel

Consider two cells in series. Let ε₁, r₁ be the emf and internal resistance of first cell. Similarly ε₂, r₂ be the emf and internal resistance of second cell. Let I be the current in this circuit.
From the figure, the P.d between A and B
V_A – V_B = ε₁ – Ir₁ _____(1)
Similarly P.d between B and C
V_B – V_C = ε₂ – Ir₂ ______(2)
Hence, P.d between the terminals A and C
V_AC = V_A – V_C = V_A – V_B + V_B – V_C
V_AC = [V_A – V_B] + [V_B – V_C]
when we substitute eqn. (1) and (2) in the above equation.
V_AC = ε₁ – Ir₁ + ε₂ – Ir₂ V_AC = (ε₁ – ε₂) – I(r₁ + r₂)
V_AC = ε_eq – Ir_eq
where ε_eq = ε₁ + ε₂, and r_eq = r<sub1 + r₂
The rule of series combination:

1. The equivalent emf of a series combination of n cells is the sum of their individual emf.
2. The equivalent internal resistance of a series com-bination of n cells is just the sum of their internal resistances.

Cells in parallel:

Consider two cells connected in parallel as shown in figure. ε₁, r₁ be the emf and internal resistance of first cell and ε₂, r₂ be the emf and internal resistance of second cell. Let I₁ and I₂ be the current leaving the positive electrodes of the cells.
Total current flowing from the cells is the sum of I₁ and I₂.
ie. I = I₁ + I₂ ______(1)
Let V_B1 and V_B2 be the potential at B₁ and B₂ respectively. Considering the first cell, P.d between B₁ and B₂.

Considering the second cell, P.d between B₁ and B₂

Substituting the values I₁ and I₂ in eq.(1), we get


If we replace the combination by a single cell between B₁ and B₂, of emf and ε_eq and internal resistance r_eq, we have
V = ε_eq – Ir_eq ______(3)
The eq(2) and eq(3) should be same.

The above equation can be put in a simpler way.

If there are n cells of emf ε₁, ε₂,………..ε_n and internal
resistance r₁, r₂………..r_n respectively, connected in parallel.

Kirchoff’s Rules
1. First law (Junction rule): The total current entering the junction is equal to the total current leaving the junction.
Explanation:

Consider a junction ‘O’. Let I₁ and I₂ be the incoming currents and I₁, I₄ and I₅ be the outgoing currents.
According to Kirchoff’s first law,

2. Second law (loop rule): In any closed circuit the algebraic sum of the product of the current and resistance in each branch of the circuit is equal to the netjemf in that branch.

OR

Total emf in a closed circuit is equal to sum of voltage drops

Explanation: Consider a circuit consisting of two cells of emf E₁ and E₂ with resistances R₁, R₂ and R₃ as shown in figure. Current is flowing as shown in figure
Applying the second law to the closed circuit ABCDE₁A.
-I₃R₃ + E₁ + -I₁R₁ = 0
Similarly for the closed loop ABCDE₂A.
-I₂R₂ + -I₃R₃ + E₂ = 0
For the closed loop AE₂DE₁A
-I₁R₁ + I₂R₂ + -E₂ + E₁ = 0
Note:

• Voltage drop in the direction of current is taken as negative (and vice versa).
• emf is taken as positive, if we go -ve to +ve terminal (and vice versa)

Wheatstone’s Bridge
Four resistances P, Q, R, and S are connected as shown in figure. Voltage ‘V’ is applied in between A and C. Let I₁, I₂, I₃ and I₄ be the four currents passing through P, R, Q, and S respectively.

Working:
The voltage across R
When key is closed, current flows in different branches as shown in figure. Under this situation
The voltage across P, V_AB = I₁P
The voltage across Q, V_BC = I₃Q __(1)
The voltage across R, V_AD = I₂R
The voltage across S, V_DC = I₄S
The value of R is adjusted to get zero deflection in galvanometer. Underthis condition,
I₁ = I₃ and I₂ = I₄ _____(2)
Using Kirchoffs second law in loopABDA and BCDB, weget
V_AB = V_AD ______(3)
and V_BC = V_DC _______(4)
Substituting the values from eq(1) into (3) and (4), we get
I₁P = I₂R ______(5)
and I₃Q = I₄S _____(6)
Dividing Eq(5) by Eq(6)

[since I₁ = I₃ and I₂ = I₄]
This is called Wheatstone condition.

Meter Bridge
Uses: Meter Bridge is used to measure unknown resistance.
Principle: It works on the principle of Wheatstone bridge condition (P/Q=R/S).

Circuit details:
Unknown resistance X’ is connected in between A and B. Known resistance (box) is connected in between B and C. Voltage is applied between A and C. A100cm wire is connected between A and C. Let r be the resistance per unit length. Jockey is connected to ‘B’ through galvanometer.
Working: A suitable resistance R is taken in the box. The position of jockey is adjusted to get zero deflection.
If ‘l’ is the balancing length from A, using Wheatstone’s condition,

knowing R and l, we can find X (resistance of wire)
Resistivity: Resistivity of unknown resistance (wire) can be found from the formula
\(\rho=\frac{\pi r^{2} X}{l}\)
Where r (the radius of wire) is measured using screw gauge. l (the length of wire) is measured using meter scale
Note: Meter bridge is most sensitive when all the four resistors are of the same order

Potentiometer
(a) Comparison of e.m.f of two cells using potentiometer:

Principle: Potential difference between two points of a current carrying conductor (having uniform thickness) is directly proportional to the length of the wire between two points.

Circuit details: A battery (B₁), Rheostat and key are connected in between A and B. This circuit is called primary circuit. Positive end of E₁ and E₂ are connected to A and other ends are connected to a two way key. Jockey is connected to a two key through galvanometer. This circuit is called secondary circuit.

Working and theory: Key in primary circuit is closed and then E₁ is put into the circuit and balancing length l₁ is found out.
Then, E₁ α l₁ ______(1)
Similarly, E₂ is put into the circuit and balancing length (l₂ ) is found out.
Then, E₂ α l₂ _______(2)
Dividing Eq(1) by Eq(2),
\(\frac{E_{1}}{E_{2}}=\frac{l_{1}}{l_{2}}\) _____(3)

(b) Measurement of internal resistance using potentiometer:
Principle: Potential difference between two points of a current carrying conductor (having uniform thickness) is directly proportional to the length of the wire between two points.

Circuit details: Battery B₁, Rheostat and key K1 are connected in between A and B. This circuit is called primary.

In the secondary circuit a battery E having internal resistance ‘r’ is connected . A resistance box (R) is connected across the battery through a key (K^{2). Jockey is connected to battery through galvanometer.}

Working and theory : The key (K₁) in the primary circuit is closed and the key is the secondary (K₂) is open. Jockey is moved to get zero deflection in galvanometer. The balancing length l₁ (from A) is found out.
Then we can write.
E₁ α l₁ _____(1)
Key K₂ is put in the circuit, corresponding balancing length (l₂) is found out. Let V be the applied voltage, then
V₁ α l₁ _____(2)
‘V’ is the voltage across resistance box.
Current through resistance box
ie, voltage across resistance,
V = \(\frac{E R}{(R+r)}\) ____(3)
Substituting eq (3) in eq (2),
\(\frac{E R}{(R+r)} \alpha l_{2}\) ____(4)
Dividing eq (1) by eq (4),

Question 1.
Why is potentiometer superior to voltmeter in measuring the e.m.f of a cell?
Answer:
Voltmeter takes some current while measuring emf. So actual emf is reduced. But potentiometer does not take current at null point and hence measures actual e.m.f. Hence potentiometer is more accurate than voltmeter.

Students can Download Chapter 7 The p Block Elements Notes, Plus Two Chemistry Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus Two Chemistry Notes Chapter 7 The p Block Elements

The p-block – Elements of group 13 to 18 of the periodic table. The outer electronic configuration of a p-block element is ns²np^1-6.

Anomalous behaviour of the first element of a group: This is due to

1. Small in size
2. High electronegativity,
3. High ionisation enthalpy and
4. Non-availability of d – orbitals.

Diagonal Relationship:
In some cases, the first element of a group resembles diagonally with the element of the next group and of the next period.

Group 15 – Elements – Nitrogen Family:
Elements are – N, P, As, Sb, Bi
N₂ comprises 78% by volume of the atmosphere. N and P are essential constituents of animals and plants. N – Present in proteins, P – Present in bones.

Characteristics:
1. Atomic radii increases with increase in Atomic Number.

2. Ionisation Enthalpy decreases down the group due to gradual increase in atomic size. Because of the extra stable half-filled p orbitals electronic configuration and smaller size, the ionisation enthalpy is less than that of group 14 elements in the corresponding periods.

3. Electronegativity decreases down the group.

Physical Properties:
All are polyatomic, metallic character increases from N to Bi, density increases from N to Bi, M.P. and B.P. increases down the group, except N all other elements show allotropy.

Chemical Properties:
Oxidisation states and trends in chemical reactivity:
The common oxidation states of 15 group elements are (-3), (+3) and (+5). The stability of +5 oxidisation state decreases and that of +3 state increases down the group due to inert pair effect. Nitrogen exhibits +1, +2, +4 oxidation states also when it react with O₂.

The maximum covalence of N restricted to 4 since only 4 orbitals (one S and three P) are available for bonding.

Anomalous Properties of Nitrogen:
It is due to its small size, high electronegativity, high ionisation enthalpy and non-availability of ‘d’ orbitals. Nitrogen has unique ability to form pπ – pπ multiple bond. It cannot form dπ – pπ bond. P and A scan form dπ – dπ bond.

(i) Reactivity towards hydrogen:
EH₃ hydrides, the central atom is sp³ hybridised, molecules assume trigonal pyramidal geometry with a lone pair on the central atom. Stability-decreases from NH₃ to BiH₃.

This is because, down the group the E-H bond dissociation enthalpy decreases due to increase in size of the central atom. Consequently, reducing character increases from NH₃ to BiH₃. The basicity decreases in the order NH₃ > PH₃ > AsH₃ > SbH₃> BiH₃.

As the electro negativity of the central atom decreases on moving down the group, the bond pair-bond pair repulsion decreases. Hence the bond angle decreases in the order NH₃ > PH₃ > AsH₃.

(ii) Reactivity towards oxygen:
They form E₂O₃ & E₂O₅ type oxides. The oxide in the higher oxidisation state of the element is more acidic than that in lower oxidation state.

(iii) Reactivity towards halogens:
They form EX₃ and EX₅ type halides. Nitrogen does not form pentahalide due to non-availability of d-orbital.

(iv) Reactivity towards Metals:
They react with some metals exhibiting – 3 oxidation state, e.g. Calcium nitrate (Ca₃N₂), Calcium phosphide (Ca₃P₂), Sodium arsenide (Na₃As₂).

Dinitrogen (N₂):
It is produced commercially by the liquefaction and fractional distillation of air.
In laboratory, N₂ is prepared by

NH₄Cl(aq) + NaNO₂(aq) → N₂(g) + 2 H₂O(l)+ NaCl(aq)

Properties:
Colourless, odourless, non-toxic gas; inert at room temperature because of high bond enthalpy of N ≡ N.

Uses:
Manufacture of NH₃, liquid N₂ is used as refrigerant to preserve biological materials, food items and in cryosurgery.

Ammonia:
Laboratory preparation:
2NH₄Cl + Ca(OH)₂ → 2NH₃ + 2H₂O + CaCl₂
(NH₄)₂SO₄ + 2NaOH → 2NH₃ + 2H₂O + Na₂SO₄

Industrial (large scale) preparation by Haber’s process:
N₂(g) + 3H(g) ⇌ NH₃(g); Δ_fH^Ⓗ = -46.1 kJ/mol^-1 Catalyst used earlier- spongy iron with molybdenum promoter. Catalyst used now – iron oxide with small amounts of K₂O and Al₂O₃.

High pressure and low temperature will favour the formation of NH₃ as the forward reaction is exothermic and is accompanied by decrease in number of moles (Le Chatelier’s principle). Hence, a pressure of 200 × 10⁵ Pa (about 200 atm) and a temperature of ~ 700 K are employed to increase the yield of NH₃.

Properties:
Colourless, pungent smelling gas, trigonal pyramidal geometry, highly soluble in water.
NH₃(g) + H₂O(l) \(\rightleftharpoons\) NH⁺₄(aq) + OH^–(aq)
Lewis base – due to the presence of a lone pair of electrons on N. It can form complex compounds with metal ions. This finds application in the detection of
Cu²⁺ and Ag⁺.

Uses:
To produce various nitrogeneous fertilizers, manufacture of inorganic nitrogen compounds (e.g. HNO₃), liquid NH₃ is used as a refrigerant.

Oxides of Nitrogen:

1. Dinitrogen oxide (N₂O) or laughing gas – Oxdation state (+1) – Colourless gas, neutral.
2. Nitrogen monoxide(NO) – Oxdation state (+2) colourless gas, neutral.
3. Dinitrogen Trioxide(N₂O₃) – Oxdation state (+3), blue solid, acidic in nature.
4. Nitrogen dioxide(NO₂) – Oxdation state (+4) brown gas, acidic. It contains odd number of valence electrons. On dimerisation, it is converted to stable N₂O₄ molecule with even number of electrons.
5. Dinitrogen tetroxide(N₂O₄) – Dimer of NO₂ – Oxdation state (+4), colourless solid/liquid, acidic.
6. Dinitrogen pentoxide (N₂O₅) – Oxdation state (+5), colourless solid, acidic.

Nitric Acid:
It is the most important oxoacid of N.
Laboratory preparation:
KNO₃/NaNO₃ + H₂SO₄(conc.) → KHSO₄/NaHSO₄ + HNO₃
Industrial preparation – Ostwald’s process:
(1) NH₃ oxidised to NO by air.

(2) NO is converted to NO₂
2NO(g) + O₂(g) ⇄ 2NO₂(g)

(3) NO₂ dissolved in water to give HNO₃
3NO₂(g) + H₂O(l) → 2HNO₃ (aq) + NO(g)

Properties:
Colourless liquid, strong acid in aqueous solution. Concentrated HNO₃ is a strong oxidising agent and attacks most metals except noble metals like Au and Pt. The products of oxidation depend upon the concentration of the acid, temperature and the nature of the material undergoing oxidation, e.g.

• 3Cu + 8HNO₃(dilute) → 3Cu(NO₃)₂ + 2NO + 4H₂O
• Cu + 4HNO₃(conc.) → CuCu(NO₃)₂ + 2NO₂ + 2H₂O
• 4Zn + 10HNO₃(dilute) → 4Zn(NO₃)₂ + 5H₂O + N₂O
• Zn + 4HNO₃(conc.) → Zn(NO₃)₂ + 2H₂O + 2N₂O

Some metals (e.g., Cr, Al) do not dissolve in concentrated nitric acid because of the formation of a passive film of oxide on the surface.

Structure:
In the gaseous state, HNO₃ exists as a planar molecule.

Uses:
Manufacture ammonium nitrate (fertilizer), preparation of explosives, preparation of nitroglycerine, pickling of stainless steel, etching of metals, oxidiser in rocket fuels.

Phosphorus:
Allotropic forms – White P, red P and black P

White Phosphorus:
Transient white waxy solid, poisonous, insoluble in water, soluble in CS₂, glows in dark (chemiluminescence), kept underwater, less stable and therefore more reactive than other solid phases under normal conditions because of angular strain in discrete tetrahedral P₄ molecules (angle 60°), readily catches fire in air and gives dense while fumes of P₄O₁₀.
P₄ + 5O₂ → P₄O₁₀

Red Phosphorus:
Obtained by heating white P at 573 K in an inert atm for several days, possesses iron grey lustre, odourless, non-poisonous, less reactive than white P, does not glow in dark, polymeric consisting of chains of P₄ tetrahedra.

Black Phosphorus:
Obtained when red P is heated under high pressure, two forms α – black phosphorus (formed when red P is heated in a sealed tube at 803 K) and β – black phosphorus (prepared by heating white P at 473 K under high pressure).

Phosphine (PH₃):
Prepared by the reaction of calcium phosphide with water or dilute HCl.
Ca₃P₂ + 6H₂O → 3Ca(OH)₂ + 2PH₃
Ca₃P₂ + 6HCl → 3CaCl₂ + 2PH₃

Laboratory preparation:
By heating white P with con centrated NaOH solution in an inert atmosphere of CO₂.
P₄ + 3NaOH + 3H₂O → PH₃ + 3NaH₂PO₂

Properties:
Colourless gas with a rotten fishy smell, highly poisonous, weakly basic, the structure is similar to NH₃ and gives phosphonium compounds with
acids. PH₃ + HBr → PH₄Br
Uses: in Holme’s signals, in smoke screens.

Phosphorus Halides:
It forms two types of halids PX₃ and PX₅ (X = F, Cl, Br)

Phosphorus Trichloride (PCl₃):
Obtained by passing dry Cl₂ over heated white P.
P₄ + 6Cl₂ → 4PCl₃

Or, by the action of thionyl chloride on white P,
P₄ + 8SOCl₂ → 4PCl₃ + 4SO₂ + 2S₂Cl₂

Properties
Colourless oily liquid, hydrolyses in the presence of moisture giving fumes of HCl.
P₄ + 3H₂O → H₃PO₃ + 3HCl
It has pyrimidal shape and P is sp3 hybridised.

Phosphorus Pentachloride (PCl₅):
Preparation:
White P₄ + 10Cl_2(dry) → 4PCl₅

Properties:
yellowish white powder. In moist air it hydrolysed giving POCl₃ and finally gets converted to phosphoric acid (H₃PO₄)
PCl₅ + H₂O → POCl₃ + 2HCl
POCl₃ + 3 H₂O → H₃PO₄ + 3 HCl
In gaseous and liquid phases, the shape of the molecule is trigonal bipyramidal. There are two types of P-Cl bonds, equatorial bond and axial bond. Axial bonds are longer than equitorial bonds due to more repulsion. In solid state it exits as ionic solid, [PCl₄]⁺[PCl₆]^–.

Oxoacids of Phosphorus:

• Hypophosphorous/Phosphinic acid(H₃PO₂) – Monobasic
• Orthophosphorous/Phosphonic acid(H₃PO₃) – Dibasic
• Pyrophosphorous acid(H₄P₂O₅) – Dibasic
• Hypophosphoric acid(H₄P₂O₆) – Tetrabasic
• Orthophosphoric acid(H₃PO₄) – Tribasic
• Pyrophosphoric acid(H₄P₂O₇) – Tetrabasic
• Metaphosphoric acid(HPO₃)_n – Tribasic

The p-H bonds are not ionisable and have no role in basicity. Only those H atoms in P-OH form are ionisable and cause basicity.

These acids in +3 oxidation state of P tend to disproportionate to higher and lower oxidation states, e.g. Orthophosphorous acid on heating disproportionates to give orthophosphoric acid (P in +5 state) and phosphine

The acids with P-H bond .have strong reducing property, e.g. H₃PO₂. It reduces AgNO₃ to Ag.

Structure of Oxoacids:

Group 16 Elements (Chalcogens):
O, S, Se, Te and Po.

1. Occurrence:
O₂ – Most abundant element on earth crust (46.6%), dry air contains 21% by volume. S – Present as sulphates, sulphides (e.g. CaSO₄, PbS, ZnS). Se &Te-in metal selenides and tellurides, Po-radio active, formed by the decay of thorium and uranium minerals.

2. 6 General electronic configuration-ns²np⁴. In group:
Atomic and ionic radii increases, ionisation enthalpy, electron gain enthalpy and electronegativity decreases – O has the highest electronegativity next to F.

3. Physical Properties:
O is a diatomic gas, non metal. S-solid, non-metal. Se and Te are metalloids. Po-radioactive metal.

4. Chemical Properties:
Oxidation states and trends in chemical activity – exhibits variable oxidation states, stability of -2 oxidation state decreases down the group. O-shows +2 in OF₂, -1 in peroxides and – 2 in other compounds. Other elements show +2, +4, +6 states.

5. Anomolous Behaviour of Oxygen:
It is due to small size high electronegativity, non availability of d-orbital and high polarising power.

(i) Reactivity with Hydrogen:
group 16 elements form H₂E type hydrids (E = O, S, Se, Te, Po). Their acidic character increases from H₂O to H₂Te due to decrease in H-E bond dissociation enthalpy. All hydride except H₂O posses reducing property. Reducing nature increases from H₂S to H₂Te.

Due to small size and high electro naegativity of oxygen, H₂O molecules are highly associated through hydrogen bonding resulting in its liquid state and high boiling point.

While, due to large size and low electronegativity of S association through hydrogen bonding is hot possible in H₂S. Hence it exists as a gas and has low boiling point than H₂O.

(ii) Reactivity with Oxygen:
They form EO₂ & EO₃ type oxides. Ozone, O₃ and SO₂ are gases. Both type of oxides are acidic in nature.

(iii) Reactivity Towards the Halogens:
They form EX₂, EX₄ and EX₆ type halides. The stability of halides decrease in the order F^– > Cl^– > Br > l^–

Dioxygen (O₂):
Preparation:
(i) Heating KClO₃, KMnO₄, KNO₃ etc.

(ii) Thermal decomposition of metal oxides.
2Ag₂O → 4Ag + O₂
2PbO₂ H → 2PbO + O₂

(iii) Decomposition of H202
2H₂O₂ → 2H₂O + O₂.

Large scale preparation:
Electrolysis of water, O₂ liberated at anode.

Properties:
Colourless, odourless gas; paramagnetic, directly reacts with nearly all metals except Au and Pt.

Simple Oxides:
Binary compound of O with another element, e.g. MgO, Al₂O₃. Basic oxide – oxide that combine with water give a base. e.g. MgO. Acidic oxide – oxide that combine with water to give acid, e.g. SO₂, CO₂.
SO₂ + H₂O → H₂SO₃
In general, metallic oxides are basic and non-metallic oxides are acidic.

Ozone (O₃):
Allotropic form of O, too reactive, prepared by passing a slow dry stream of O₂ through a silent electrical discharge.
3O₂ → 2O₃
ΔH = +142 kJ mol^-1

Properties:
Pure O₃ is a pale blue gas, dark blue liquid and violet-black solid, thermodynamically unstable compared to O₂.

Oxidising property:
Due to the ease with which it liberates atoms of nascent oxygen 03 acts as a powerful oxidising agent.
O₃ → O₂ + [O]
e.g. It oxidises lead sulphide to lead sulphate.
PbS(s) + 4O₃(g) → PbSO₄(s) + 4O₂(g)

Estimation of O₃:
When O₃ reacts with excess of Kl solution buffered with a borate buffer (pH 9.2), l₂ is liberated which can be titrated against a standard solution of sodium thiosulphate.
2l^–(aq) + H₂O(l) + O₃(g) → 2OH^–(aq) + l₂(s) + O₂(g)

Uses:
As a germicide, disinfectant and for sterilising water; for bleaching oils, ivory, starch etc. as oxidising agent in the manufacture of KMnO₄.

Sulphur-Allotropic Forms:
Rhombic Sulphur (α – Sulphur):
yellow, insoluble in water, dissolve to some extent in benzene and alcohol, readily soluble in CS₂.

Monoclinic Sulphur (β – Sulphur):
Soluble in CS₂, needle shaped crystals.

Structure:
They exists as S₈ molecules, the S₈ ring is puckered and has a crown shape. The cylco-S₆ ring adopts a chair form.

Sulphur Dioxide (SO₂):
Preparation:
1. Burning of S in air
S(s) + O₂(g) → SO₂(g)

2. Treating sulphite with diluted H₂SO₄.
SO₃^2- + 2H⁺ → H₂O + SO₂

Properties:
Colourless gas with pungent smell, highly soluble water, when passed through water forms sulphurous acid.
SO₂(g) + H₂O(l) → H₂SO₃(aq)

React with NaOH:
2NaOH + SO₂ → Na₂SO₃ + H₂O

Other reactions:
3SO₂ + Cl₂ → SO₂Cl₂

Users:
In pertroleum refining and sugar industry, in bleaching wool and silk, in manufacturing H₂SO₄.

Oxoacids of Sulphur:
Sulphur forms a number of oxoacids such as H₂SO₃, H₂SO₄, H₂S₂O₃, H₂S₂O₇

Manufacture of Sulphuric Acid:
Sulphuricacid is known as king of chemicals. It is manufactured by Contact Process.

Steps Involved:
(i) Burning of S or Sulphide ores in air to form SO₂

(ii) Conversion of SO₂ to SO₃ by the reaction with O₂ in presence of V₂O₅ catalyst.

ΔH = -196.6 KJ mol^-1
Low temperature (720 K) and high pressure (2 bar) are the favourable conditions for maximum yield.

(iii) Absorption of SO₃ in H₂SO₄ to give oleum (H₂S₂O₇)
SO₃ + H₂SO₄ → H₂S₂O₈
Dilution of oleum with water gives H₂SO₄ of desired concentration. H₂S₂O₇ + H₂O → 2 H₂SO₄

Properties:
Colourless, oily liquid, dissolves in water with the evolution of large quantity of heat, dibasic acid, in aqueous solution, it ionises in two steps:
H₂SO₄(aq) + H₂O(l) → H₃O⁺(aq) + HSO₄^– (aq)
HSO₄^–(aq) + H₂O(l) → H₃O⁺(aq) + SO₄^2-(aq)
Concentrated H₂SO₄ is a strong dehydrating agent.

Uses:
Manufacture of fertilisers; petroleum refining; manufacture of pigments, paints, dyestuff; detergent industry; storage batteries; laboratory reagent

Group 17 Elements (Halogens): F, Cl, Br, I and At (radio active), highly reactive non-metallic elements.

1-6 Occurrence:
F-in fluorides (CaF₂, Na₃AIF₆). Sea water contains chlorides, bromides and iodides of Na & K, electronic configuration – ns²np⁵, in a group from top to bottom atomic and ionic radii increases, ionisation enthalpy decreases.

Electron gain enthalpy – halogen have maximum negative electron gain enethalpy. Cl has highest electron gain enthalpy. Electro negativity decreases down the group. F is the most electronegative element in the periodic table.

Physical Properties:
F₂, Cl₂ – gases, Br₂ – liquid and l₂ – solid. F₂ and Cl₂ react with water Br₂ and l₂ sparingly soluble in water.

Oxidation States and Trends in Chemical Reactivity:
All the halogens exhibit-1 oxdn. state. But, Cl, Br and I exhibit +1, +3, +5 and +7 also. They react with metals and non-metals to form halides. The reactivity of the halogens decreases down the group.

Anomalous Behaviour of Fluorine:
It is due to smaller in size, high electronegativity, low F-F bond dissociation enthalpy and non-availability of d-orbitals, due to which it cannot expand its octet. It exhibits only-1 oxidation state.

(i) Reactivity Towards Hydrogen:
All form hydrogen halides (HX) which dissolve in water to form hydrohalic acids. The acidic strength of acids:
HF < HCl < HBr < Hl .The stability of halides decreases down the group due to decrease in (H-X) dissociation enthalpy in the order: H-F > H-Cl > H-Br > H-l.

(ii) Reactivity Towards Oxygen:
They form many oxides but most of them are unstable. Fluorine form OF₂ and O₂F₂. Chlorine form oxides Cl₂O, ClO₂, Cl₂O₆ and Cl₂O₇, which are highly reactive oxidising agents, ClO₂ is used as a bleaching agent for paper pulp, textiles.

(iii) Reactivity Towards Metals:
Metal halides are formed,
e.g. Mg(s) + Br₂(l) → MgBr₂(s)

(iv) Reactivity of Halogens Towards Other Halogens:
Halogens combine amongst themselves to form a number of compounds known as interhalogens. Five types: XX’, XX3, XX’5, XX’7 where X is a halogen of larger size and X’ of smaller size.

Chlorine:
Preparation:
(i) By heating manganese dioxide with concentrated HCl.
MnO₂ + 4HCl → MnCl₂ + 2H₂O + Cl₂

(ii) By the action of HCl on KMnO₄.
2KMnO₄ + 16HCl → 2KCl + 2MnCl₂ + 8H₂O + 5Cl₂

Manufacture:
(i) Deacon’s Process – By oxidation of HCl gas by atm oxygen in the presence of CuCl₂ at 723K.

(ii) Electrolytic process
 (liberated at anode)

Properties:
Greenish yellow gas with pungent and suffocating odour, reacts with metal, and non metals

With excess NH₃, Cl₂ gives N₂ and NH₄Cl whereas with excess Cl₂, NH₃ gives NCl₃ (explosive) and HCl.

With cold and dilute alkalies chlorine produces a mixture of chloride and hypochlorite but with hot and concentrated alkalies it gives chloride and chlorate.

With dry slaked lime, it gives bleaching powder.
2Ca(OH)₂ + 2Cl₂ → Ca(OCl)₂ + CaCl₂ + 2H₂OCl₂ is a powerful bleaching agent.
Cl₂ + H₂O → 2HCl + [O]
Coloured substance + [0] → colourless substance

Uses:
For bleaching wood pulp, cotton and textiles; for the preparation of insectiside, pesticides and other organic solvents, e.g. CHCl₃, DDT, BHC etc.

Hydrogen Chloride (HCl):
Preparation:

HCl gas is dried by passing through a cone. H₂SO₄.
Properties :
Colourless and pungent smelling gas, soluble in water and ionises as follows:
HCl + H₂O → H₃O⁺ + Cl^–
It reacts with NH₃ to give white fumes of NH₄Cl.
NH₃ + HCl → NH₄Cl
It decomposes salt of weaker acids.
Na₂CO₃ + 2HCl → 2NaCl + H₂O + CO₂
NaHCO₃ + HCl → NaCl + H₂O + CO₂

Uses: manufacture of Cl₂, NH₄Cl and glucose; for extracting glue.

Oxoacids of Halogen:
Due to high electronegativity and smaller in size fluorine forms only one oxoacid, HOF known as fluoric acid or hypofluorous acid.

Some oxoacids of Chlorine:

• Hypochlorous acid: HOCl (Cl in +1 state)
• Chlorous acid: HClO₂ (Cl in +3 state)
• Chloricacid: HClO₃ (Cl in +5 state)
• Perchloricacid: HClO₄(Cl in +7 state).

Interhalogen Compounds:
Two different halogens react to form inter halogen compounds, e.g. ClF, ClF₃, BrF₅, IF₇

Preparation:
By the direct combination of halogens.

Properties:
Covalent molecules, diamagnetic, volatile solids or liquids at 25°C except ClF which is a gas. They are more reactive than halogens because X-X bond is weaker than X-X bond. Due to electronegativity difference the X – X bond is polarised, hence it is reactive.

Their stability increases as the size difference of the halogens increases due to increase in the polarity of the bond. e.g. IF₃ is more stable than ClF₃.

Group 18 Elements (Noble Gases):
He, Ne, Ar, Kr, Xe and Rn (radio active). Except He all other noble gas have 8 electrons in the valence shell. Due stable electronic configuration all these are gases and chemically unreactive, (exeption – Kr, Xe, Rn)

Occurrence:
All except Rn occur in the atmosphere. The main source of He-natural gas. Rn- obtained as a decay of product of Radium.

Electronic Configuration-ns²np⁶ (except He-1s² ), ionisation enthalpy-high due to stable electronic configuration-it decreases down the group, atomic radii-increases down the group, electron gain enthalpy-almost zero since no tendency to accept an electron.

Physical Properties:
Monoatomic, colourless, odourless and tasteless gases, sparingly soluble in water, very low melting and boiling points because the only type of interatomic interaction in these elements is weak dispersion forces.

Chemical Properties:
Least reactive due to stable electronic configuration, high ionisation enthalpy and more positive electron gain enthalpy.

N. Bartlett prepared Xe⁺PtF₆ by mixing PtF₆ and Xe.

(a) Xenon – Fluorine Compounds:
Xe forms three binary fluorides XeF₂, XeF₄ and XeF₆ by the direct reaction of Xe with F₂.

XeF₄^– also prepared by reaction with O₂F₂ and XeF₄. XeF₄ + O₂F₂ → XeF₆ + O₂

Structure:
(a) XeF₂ – sp³d hybridisation -linear
XeF₄ – sp³d² hybridisation – square planar
XeF₆ – sp³d³ hybridisation – distorted octahedral

(b) Xenon-Oxygen Compounds:
XeO₃: Prepared by hydrolysis of XeF₄ and XeF₆.
6XeF₄ + 12H₂O → 4Xe + 2XeO₃ + 24HF + 3O₂
XeF₆ + 3H₂O → XeO₃ + 6HF.
XeOF_4^–prepared by partial hydrolysis of XeF₆.
XeF₆ + H₂O → XeOF₄ + 2HCl

Structure:
XeO₃ – sp³ hybridisation – Pyramidal
XeOF₃ – sp³d² hybridisation – Square pyramidal

Uses of Noble Gases:
1. He – for filling airships, aeroplane tyres, in gas-cooled nuclear reactors, for providing an inert atmosphere in the welding of metals and alloys.

2. Ne – for filling discharge tubes and fluorescent bulb for advertisement purpose, in botanical gardens and greenhouses.

3. Ar – to provide inert atmosphere in high-temperature metallurgical processes, for filling electric bulbs, for handling air-sensitive substances in laboratory.

4. Xe and Kr – in light bulbs designed for special purposes.

Students can Download Chapter 2 Electric Potential and Capacitance Notes, Plus Two Physics Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus Two Physics Notes Chapter 2 Electric Potential and Capacitance

Introduction
The electric field strength is a vector quantity, while electric potential is a scalar quantity. Both these quantities are inter related.

Electrostatic Potential

1. Electric potential: The electric potential at a point is the work done by an external agent in moving a unit positive charge from infinity to that point against the electric field (without acceleration)
Explanation: If W is the work done in moving a charge ‘q’ from infinity to a point, then potential at
that point is, V = \(\frac{w}{q}\)

Potential difference: Electric potential difference between two points is the work done in moving a unit positive change from one point to other.
Potential difference between the points A and B is
V_AB = V_A – V_B
V_A and V_B are the potentials at the points A and B respectively.

Potential energy difference: Potential energy difference is the work done to bring a q charge from one point to another point with out acceleration.
Relation between potential difference and potential energy difference:

where U_A and U_B are the potential energies at the points A and B respectively.

Electric field is conservative: Electric field is conservative. A conservative field is defined as the field in which work done is zero in a complete round trip.

(or)

A conservative field is one in which work done is independent of path.

Potential Due To A Point Charge

Let P be a point at a distance Y from a charge +q. Let A be a point at a distance ‘x’ from q ,and E is directed along PA. Consider a positive charge at A. Then the electric field intensity at A’ is given by

If this unit charge is moved (opposite to E) through a distance dx, the work done dw = – Edx
[-ve sign indicates that dx is opposite to E ]
So the potential at ‘P’ is given by

Potential due to an electric dipole

Consider dipole of length ‘2a’. Let P be a point at distance r₁ from +q and r₂ from -q. Let ‘r’ be the distance of P from the centre ‘O’ of the dipole. Let θ be angle between dipole and line OP.

Therefore total potential,

From ∆ABC , we get (r₂ – r₁) = 2a cosθ
we can also take r₂ = r₁ = r (since ‘2a’ is very small) Substituting these values in equation (1), we get

Case 1: If the point lies along the axial line of the dipole, then θ = 0°

Case 2: If the point lies along the equatorial line of the dipole, then θ = 90°

V = 0

Potential Due To A System Of Charges

Consider a system of charges q₁, q₂,……,q_n with position vectors r_1P, r_2P……..,r_nP relative to some origin. The potential V₁ at P due to the charge q₁ is

where r_1P is the distance between q₁ and P. Similarly, the potential V₂ at P due to q₂,

where r_2P is the distances of P from charges q₂. By the superposition principle, the potential V at P due to the total charge configuration is the algebraic sum of the potentials due to the individual charges
ie. V = V₁ + V₂ +……+ V_n

Equipotential Surface
The surface over which the electric potential is same is called an equipotential surface.
Properties:

1. Direction of electric field is perpendicular to the equipotential surface.
2. No work is done to move a charge from one point to another along the equipotential surface.

Example:

1. Surface of a charged conductor.
2. All points equidistant from a point charge.

Equipotential surfaces for a uniform electric filed:

1. Relation Between Electric Field And Potential:

Consider two points A and B, separated by very small distance dx. Let the potential at A and B be V+ dV and V respectively. The electric field is directed from A to B.
If a unit +ve charge is moved through a distance ‘dx’ against this field, work done,
dw = -Edx _____ (1)
For unit charge dw = dv
∴ dv = – Edx
or

Electric field intensity at a point is the negative rate of change of potential with distance.

Potential Energy Of System Of Charges

1. Potential Energy of System of Two Charges:
The potential energy of a system of two charges is defined as the work done in assembling this system of charges at the given position from infinite separation.

Consider two charges q₁ and q₂ separated by distance r. Imagine q₁ to be at A and q₂ at infinity. Electric potential at B due to charge q₁ is given by

which is the work done in bringing unit positive charge from infinity to B. Therefore the work done in bringing charge q₂ from infinity to B is
W = potential difference × charge
W = (V₁ – V_∞)q₂
potential at inf infinity. V_∞ = 0
W = V₁ × q₂
\(W=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{12}}\)
This work done is stored as potential energy. Hence potential energy between the charges q₁ and q₂

2. Potential Energy of System of Three Charges:
Consider three charges q₁, q₂, and q₃ separated by distances r₁₂, r₂₃ and r₁₃.

The electric potential energy of this system is the sum of potential of each pair. Hence we can write
U = U₁₂ + U₂₃ + U₁₃

Potential Energy In An External Field

1. Potential energy of a single charge:
Consider a point O in an electric field. Let V be the electric potential at O. Hence work done in bringing a charge q from infinity to the point O is,
W = Vq.
This work done is stored in the form of electrostatic potential energy (U) of the charge q.
∴ The potential energy of the charge q in an electric field is U = Vq
Where V is the potential at that point.

2. Potential energy of a system of two charges in an electric field:
Consider an electric field. Let 1 and 2 be two points in the field and V₁ and V₂ be the potential at these points. Two charges q₁ and q₂ are located at 1 and 2.
Potential energy of the charge q₁ in the external filed is, U₁ = V₁ q₁
Potential energy of the charge q₂ in the external field is, U₂ = V₂q₂
Potential energy between the system of two charges q₁ and q₂

where r₁₂ is the distance between the charges According to the principle of super position, the potential energy of the system of two charges in an electric field is
U = U₁ + U₂ + U₁₂

3. Potential energy of a dipole in an external field:
Consider a dipole of dipole moment ‘P’ suspended in a uniform electric field of intensity ‘E’. Let θ be the angle between P and E.
Then we know torque τ = PE sinθ
Let the dipole be turned through an angle dθ
then work done dw = τdθ
= PE sinθ dθ
Total work done in rotating the dipole from θ₁ to θ₂

W = PE (cosθ₁ – cosθ₂)
This work done is stored as potential energy.

Electrostatics Of Conductors
The electrostatic properties of conductors are given below:
1. Inside a conductor, electrostatic field is zero:
In the static situation, there is no current found inside the conductor. Hence we conclude that the electric field is zero inside the conductor The vanishing of electric field inside the metal cavity is called electrostatic shielding.

2. At the surface of a charged conductor, electrostatic field must be normal to the surface at every point.

3. The interior of a conductor can have no excess charge in the static situation.

4. Electrostatic potential is constant throughout the volume of the conductor and has the same value (as inside) on its surface.

5. Electric field at the surface of a charged conductor
\(\bar{E}=\frac{\sigma}{\varepsilon_{0}} \hat{n}\)
where σ is the surface charge density and is a unit vector normal to the surface in the outward direction.

6. Electric field inside a metal cavity is zero. Vanishing of electric inside a metal cavity is called electrostatic shielding. Sensitive electrical instruments can be protected from external electricfield by placing it in a metal cavity.

Dielectrics And Polarization
Dielectrics (insulator): Dielectrics are non-conducting substances. They have no charge carriers. The molecules of dielectrics may be classified into two classes.

1. Polar molecule
2. Nonpolar molecule

Electric field due to a dipole at a point on the perpendicular bisector of the dipole (at a point on the equatorial line).

Consider a dipole of dipole moment P = 2aq. Let ‘S’ be a point on its equatorial line at a distance ‘r’ from its centre. The magnitudes of electric field at ‘S’ due to +q and -q are equal and acts as shown in figure. To find the resultant electric field resolve.

Their normal components cancel each otherwhere as their horizontal components add up to give the resultant field at ‘S’.
E = E_Acos θ + E_Bcos θ = 2 E_B cos θ

The direction of the field due to the dipole at a point on the equatorial line is opposite to the direction of dipole moment.

1. Dielectrics in external electric field
(a) Nonpolar dielectrics in external field:

Considers nonpolar dielectrics in an external electricfield. In electricfield, the positive and negative changes of a nonpolar molecule are displaced in opposite directions. Thus dipole moment is induced in a nonpolar molecule. The induced dipole moments of different molecules add up giving a net dipole moment.

(b) Polar dielectrics in external electric field:

The permanent dipoles in a polar dielectrics are arranged randomly. So total dipole moment is zero. But when we apply external electric field, the individual dipole tends to align in the direction of electricfield. The induced dipole moments of different molecules add up giving a net dipole moment.

Electric susceptibility: Non-polar dielectrics and polar dielectrics can produce net dipole moment in the external electric field. The dipole moment per unit volume is called polarization and is denoted as P. For linear isotropic dielectrics.
\(\bar{P}=\chi_{0} \bar{E}\)
where χ_e is a constant and is known as the electric susceptibility of the dielectric medium.
How does the polarized dielectric modify the external field inside it?

Consider a dielectric slab placed inside a uniform external electric field E₀. This field produces a uniform polarization as shown in the figure. Any region inside the dielectric, the net charge is zero.

This is due to the cancellation of positive charge of one dipole with negative charge of adjacent dipole. But the positive ends of the dipole do not cancel at right surface and the negative ends at the left surface.

This surface charges (-σ_p and +σ_p) produce a field \(\left(\vec{E}_{i n}\right)\) opposite to the external field. Hence total electric field is reduced inside the dielectric field which is shown in the figure below.
ie; E₀ + E_in ≠ 0

How does a metal modify the external electric field applied on it?

When a conductor placed in a electric field, the free charges are moved in opposite direction as shown in figure. This rearrangement of charges in a metal produce an internal field (E_in) inside the metal. This internal field cancels the external field. Thus the net electric field inside the metal becomes zero.
ie; E₀ + E_in = 0

Capacitors And Capacitance
Capacitor: Capacitor is a system of two conductors separated by an insulator for storing electric charges.
Capacitance of a capacitor:

Consider two conductor having charges +Q and -Q and potentials V₁ and V₂. The amount of charge Q on a plate is directly proportional to the potential difference (v₁ – v₂) between the plates,
ie. Q α V₁ – V₂
(or) Q α V (where V = V₁ – V₂)

The constant C is called the capacitance of the capacitor. If V = 1, we get Q = C. Hence capacitance of a capacitor may be defined as the amount of charge required to raise the potential difference between two plates by one volt.
Dielectric strength:
What happens to the charge stored in capacitor when the p.d. between two plates increases?
When the p.d. between two plates increases, electric field in between two plates increases. This high electric field can ionize the surrounding air (or medium) and accelerate the charges to the oppositely charged plates and neutralize the charge on the plate. This is called electric break down.

The maximum electric field that a dielectric medium can withstand without break down (of its insulating property) is called its dielectric strength. The dielectric strength of air is 3 × 10⁶ v/m.

The Parallel Plate Capacitor
Electric field due to a capacitor:

Consider a parallel plate capacitor consists of two large conducting plates 1 and 2 separated by a small distance d. Let +σ and -σ be the surface charge densities of first and second plates respectively. (Here, we take, electric field towards right is taken as positive and left as negative.)
Region I: This region lies above plate 1.
E = E₊ + E_– ie.

Region II: This region lies below the plate 2.
E = E_– + E₊ ie.

E = 0
Electric field in between two plates: In the inner region between the plates 1 and 2, the electric field due to two charged plates add up.

(a) Expression for capacitance of a capacitor: Potential difference between two plates
V= Ed

Effect Of Dielectric On Capacitance

Consider a capacitor of area A and charge densities +σ and -σ. Let d be the distance between the plates. If a dielectric slab is placed inside this capacitor, it undergoes polarization. Let +σ_p and -σ_p be polarized charge densities due to polarization.
Due to polarization electric field in between the plate becomes
\(E=\frac{\sigma}{K \varepsilon_{0}}\) _____(1)
The potential difference between the plates,
V = Ed _____(2)
Sub (1) in (2)
\(\mathrm{V}=\frac{\sigma}{\mathrm{K} \mathrm{s}_{0}} \mathrm{d}\)
Then the capacitance of capacitor

The product ε₀ K is the permittivity of the medium.

Combination Of Capacitors
1. Capacitors in series: Let three capacitors C₁, C₂ and C₃ be connected in series to p.d of V. Let V₁, V₂ and V₃ be the voltage across C₁, C_2, and C₃.

The applied voltage can be written as
V = V₁ + V₂ + V₃ ______(1)
Charge ‘q’ is same as in all the capacitor. So,

Substituting these values in (1),

If these capacitors are replaced by a equivalent capacitance ‘C’, then
V = \(\frac{q}{C}\)
Hence eq(2) can be written as

Effective capacitance is decreased by series combination.

2. Capacitors in parallel:

Let three capacitors C₁, C₂ and C₃ be connected in parallel to p.d of V. Let q₁, q₂, and q₃ be the charges on C₁, C₂ and C₃.
If ‘q’ is the total charge, then’q’can be written as
q = q₁ + q₂ + q₃
But q₁ = C₁V, q₂ = C₂V and q₃ = C₃V
Hence eq (2) can be written as
CV = C₁V + C₂V + C₃V

Effective capacitance increases in parallel connection.

Energy Stored In A Capacitor
Energy of a capacitor is the work done in charging it. Consider a capacitor of capacitance ‘C’. Let ‘q’ be the charge at any instant and ‘V’ be the potential. If we supply a charge ‘dq’ to the capacitor, then work done can be written as,
dw = Vdq
dw = \(\frac{q}{C}\)dq (since V = \(\frac{q}{C}\))
∴ Total work done to charge the capacitor (from ‘0’ to ‘Q’) is

But Q = CV
W = \(\frac{1}{2}\) CV²
This work done is stored in the capacitor as electric potential energy.
∴ Energy stored in the capacitor is,

Van De Graff Generator
Van de Graff generator is used to produce very high voltage.
Principle: If two charged concentric hollow spheres are brought in to contact, charge will always flow from inner sphere to the outer sphere.
Construction and working:

The vande Graff generator consists of a large spherical metal shell, placed on an insulating stand. Let p₁ and p₂ be two pulleys. Pulley p₁ is at the center of the spherical shell S. A belt is wound around two pulleys p₁ and p₂. This belt is rotated by a motor. Positive charges are sprayed by belt. Brush B₂ transfer these charges to the spherical shell. This process is continued. Hence a very high voltage is produced on the sphere.
Why does the charge flow from inner sphere to outer sphere?

Let ‘r’ and ‘R’ be the radius of inner sphere and outer sphere carrying charges q and Q respectively.
The potential on the outer sphere,
V(R) = Potential due to outer charge + potential due to inner charge

Potential on the inner sphere. V(r) = Potential due to outer charge + Potential due to inner charge

∴ Potential difference between the two spheres

The above equation shows that, the inner sphere will be always at higher potential. Hence, charge always flow from inner sphere to outer sphere.

Students can Download Chapter 1 Electric Charges and Fields Notes, Plus Two Physics Notes helps you to revise the complete Kerala State Syllabus and score more marks in your examinations.

Kerala Plus Two Physics Notes Chapter 1 Electric Charges and Fields

Introduction
You may have seen a spark (or a crackle sound), when we take off our synthetic clothes. Have you ever tried to find any explanation for this phenomenon? Do you know the reason for lightning?

The above phenomenon can be explained on the basis of static electricity. Static means anything that does not change with time. Electrostatics deals with the properties of charges at rest.

Electric Charge
It is found experimentally that the charges are of two types:

1. Positive charge
2. Negative change

The unit of charge is Coulomb (c).
Note: Positively charged body means deficiency of electrons in the body and a negatively charged body means excess of electrons.

Gold-Leaf electroscope: A simple apparatus to detect charge on a body is called a gold-leaf electroscope.

Apparatus: It consists of a vertical metal rod placed in a box. Two thin gold leaves are attached to its bottom end as shown in figure.

Working: A charged object touches the metal knob at the top of the rod. Charge flows on to the leaves and they diverge. The degree of divergence is an indicator of the amount of charge.

Conductors And Insulators
Conductors: Conductors are those substances which allow passage of electricity through them.
Insulators: Insulators are those substances which do not allow passage of electricity through them.

1. Earthing (Or) Grounding:
When a charged body bring in contact with earth, all the excess charge pass to the earth through the connecting conductor. This process of sharing the charges with the earth is called grounding or earthing. Earthing provides protection to electrical circuits and appliances.

Charging By Induction
A body can be charged in different ways.

1. Charging by friction
2. Charging by conduction
3. Charging by induction

1. Charging by friction:
When two bodies are rubbed each other, electronsin one body (in which electrons are held less tightly) transferred to second body (in which electrons are held more tightly).

Explanation: When a glass rod is rubbed with silk, some of the electrons from the glass are transferred to silk. Hence glass rod gets +ve charge and silk gets -ve charge.

2. Charging by conduction:
Charging a body with actual contact of another body is called charging by conduction.
Explanation:

If a neutral conducting body (A) is brought in contact with positively charged conducting body (B), the neutral body gets positively charged.

3. Charging by induction:
The phenomenon by which a neutral body gets charged by the presence of neighboring charged body is called electrostatic induction.
Explanation:
Step I: Place two metal spheres on an insulating stand and bring in contact as shown in figure (a).

Step II: Bring a positively charged rod near to these spheres. The free electrons in the spheres are attracted towards the rod. Hence, one side of the sphere becomes negative and the other side becomes positive as shown in the figure (b).

Step III: Separate the spheres by a small distance by keeping the rod nearto sphere A. The two spheres are found to be oppositely charged as shown in figure (c).

Step IV: Remove the rod, the charge on spheres rearrange themselves as shown in figure (d).

In this process, equal and opposite charges are developed on each sphere.

Basic Properties Of Electric Charge
1. Unlike charges attract and like charges repel.

2. Charge is conserved : Changes can neither be created nor be destroyed.
Explanation: When a glass rod is rubbed with silk, some of the electrons from the glass are transferred to silk. Hence glass rod gets +ve change and silk gets -ve changes.

3. Electric Charge is Quantized: Change on any body is the integral multiple of electronic charge. This is called quantization of charge.
i.e. q = ± ne, n = 1, 2, 3, ……….

4. Additivity of Charges: If a system contains n charges q₁, q₂, q₃,……..q_n, then the total change of the system is q₁ + q₂ + q₃ +……+q_n.

Coulomb’S Law
Statement: The force between two stationary electric charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
Explanation:

Consider two point charges q₁ and q₁. which are separated by a distance ’r’. The force between the changes.
\(\mathrm{F}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{q}_{1} \mathrm{q}_{2}}{\mathrm{r}^{2}}\)
vector form: The force F₁₂ (on the first charge by second} is given by (vector form)

Forces Between Multiple Charges
Super position principle: If the system contains a number of interacting changes, then the force on a given charge is equal to the vector sum of the forces exerted on it by all remaining charges.
Explanation:

Consider a system of three charges q₁ q₂ and q₃ as shown in figure.
The force on q₁ due to q₂
\(\overrightarrow{F_{12}}=\frac{1}{4 \pi \varepsilon_{0} r_{12}^{2}} r_{12}^{\wedge}\)
Similarly the force q₁ due to q₃
\(\overrightarrow{F_{13}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{13}^{2}} r_{13}^{\wedge}\)
The total force F₁ on q₁ (due to q₂ and q₃) can be written as

System of ‘n’ charges: If system contains ‘n’ charges, total force acting on q₁ due to all other charges.

Electric Field
The concept electric field is introduced to explain the interaction between two charges.
Electric field intensity: Strength or intensity of the electric field at any point is defined as the force acting on a unit positive charge placed at that point.
Mathematical expression of electric field intensity:

Consider a charge q (test charge) at a distance ‘r’ from a source charge Q.
The force acting on q due to Q.
\(\mathrm{F}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{Qq}}{\mathrm{r}^{2}}\)
If q = 1, the force acting on this unit charge due to Q
\(\mathrm{F}=\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathrm{Q}}{\mathrm{r}^{2}}\)
This force is called electric field intensity at a distance ‘r’ due to the charge Q.
ie; \(E=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{r^{2}}\)

1. Electric field due to a system of charges:
Consider a system of charges q₁, q₂………..q_n. Let P be point at distances r_1p, r_2p,………..r_np from charges. q₁, q₂,……..q_n respectively. According to super position principle, total electric field at ‘p’ due to all other charges,

2. Physical Significance Of Electric Field:
Question 1.
What are the importance of the concept of electric field?
Answer:

• Electric field explains the electrical environment of a system of charges.
• Electric field help us to explain the interaction between two charges at rest or in motion.

Electric Field Lines
Properties of Electric Lines of Force

(Field lines due to some simple charge configurations)

1. An electric line of force originates from positive charge and ends on negative charge.
2. The tangent drawn at a point on an electric line of force will give the direction of electric field at that point.
3. Two lines of force never intersect each other. (If they cut each other, at the point of intersection there will be two tangents. This indicates that there will be two directions of electric field at the same point which is impossible).
4. The number of electric lines of force passing normally through an area is directly proportional to the strength of the electric field.
5. The relative density of the field lines indicates the relative strength of electric field.
6. Electric field lines due to static charge never form closed loops.
7. In a uniform electric field, lines of force are parallel.

Electric Flux

Consider a closed surface. Let ∆\(\vec{S}\) be a small area element on the surface. The electric field lines (E) passes through this area element at an angle θ. Electric flux ∆Φ through an area element ∆\(\vec{S}\) is defined by

The direction of area vector d\(\vec{S}\) is perpendicular to the surface.

Electric Dipole
Electric dipole: A pair of equal and opposite charges separated by small distance is called electric dipole. Dipole moment (p): Electric dipole moment (p) is defined as product of magnitude of charge and dipole length.
Dipole moment p = q × 2a
q – charge, 2a – dipole length
Dipole moment is a vector, directed from negative to positive charge.

1. Electric field at a point on the axial line of an electric dipole: Consider an electric dipole of moment P = 2aq. Let ‘S’ be a point at a distance ‘r’ from the centre of the dipole.

Electric field at ‘S’ due to point charge at ‘A’

Directed as shown in figure. Electric field at ‘S’ due to point charge at ‘B’

Directed as shown in figure. Therefore resultant electric field at ‘S’
And its magnitude E = E_B + -E_A

P = q × 2a
We can neglect a2 because a<<r.
∴ Electric field at S,

This can be written in vector form as

The direction is along E_B.
The field due to an electric dipole is directed from negative charge to positive charge along the axial line.

2. Electric field due to a dipole at a point on the perpendicular bisector of the dipole (at a point on the equatorial line).

Consider a dipole of dipole moment P = 2aq. Let ‘S’ be a point on its equatorial line at a distance ‘r’ from its centre. The magnitudes of electric field at ‘S’ due to +q and -q are equal and acts as shown in figure. To find the resultant electric field resolve

Their normal components cancel each otherwhere as their horizontal components add up to give the resultant field at ‘S’.
E = E_Acos θ + E_Bcos θ = 2 E_B cos θ

The direction of the field due to the dipole at a point on the equatorial line is opposite to the direction of dipole moment.

3. Physical significance of dipole: The molecules of dielectrics may be classified into two classes:
(i) Polar molecules: In polar molecule, the centres of negative charges and positive charges do not coincide. Therefore they have a permanent
Example: H₂0, HCl, etc.

(ii) Nonpolar molecule: In nonpolar molecule, the centres of negative charges and positive charges coincide. Therefore they have no permanent electric dipole moment.
Example: C0₂, CH_4, etc.
Note: In the presence of external electric field, a nonpolar molecule becomes a polar molecule.

Dipole In A Uniform External Field

Consider an electric dipole of dipole moment P = 2aq kept in a uniform external electric field, inclined at an angle θ to the field direction.

Equal and opposite forces +qE and -qE act on the two charges. Hence the net force on the dipole is zero. But these two equal and opposite forces whose lines of action are different. Hence there will be a torque.
torque = any one force × perpendicular distance (between the line of action of two forces)
τ = qE × 2 a sin θ
Since P = 2aq
τ = P E sin θ
Vectorialy \(\vec{\tau}=\vec{P} \times \vec{E}\)
This torque tries to align the dipole along the direction of the external field.
Special Case:

• When θ = 0 ; τ =0
• When θ = 90; τ = PE, the maximum.

Note: In uniform electric field dipole has only rotational motion

Dipole in nonuniform electric field:
Question 2.
What happens to dipole if the applied electric field is nonuniform?
Answer:
In nonuniform electric field, the net force and torque acting on the dipole will not be zero. Hence the dipole undergoes for both translational and rotational motion.

Continuous Charge Distribution
Charges on a body may be distributed in different ways according to the nature of body. Depending upon this distribution of charge, we deal with different types of charge densities,

1. Line charge density, λ
2. Surface charge density, σ or
3. Volume charge density, ρ

1. Linear charge density (λ): Charge per unit length is called linear charge density. If ∆Q is the charge contained in a line element ∆l,
Linear charge density λ = \(\frac{\Delta Q}{\Delta l}\)

2. Surface charge density (σ): Charge per unit area is called surface charge density. If ∆Q is the charge contained in a area element ∆s, surface charge density can be written as
σ = \(\frac{\Delta Q}{\Delta S}\)

3. Volume charge density (ρ): Charge per unit volume is called volume change density. If ∆Q is the charge contained in a volume ∆v, volume charge density.
ρ = \(\frac{\Delta Q}{\Delta v}\)

Gauss’s Law
Gauss’s theorem states that the total electric flux over a closed surface is 1/ε₀ times the total charge enclosed by the surface.
Gauss’s theorem may be expressed

Proof:

Consider a charge +q .which is kept inside a sphere of radius ‘r’.

Important points regarding Gauss’s law:

• Gauss’s law is true for any closed surface.
• Total charge enclosed by the surface must be added (algebraically). The charge may be located anywhere inside the surface.
• The surface that we choose for the application of Gauss’s law is called the Gaussian surface.
• Gauss’s law is used to find electric field due to system of charges having some symmetry.
  Gauss’s law is based on the inverse square of distance. Any violation of Gauss’s law will indicate departure from the inverse square law.

Applications Of Gauss’s Law
Gauss’s law can be used to find electric field due to system of some symmetric charge configurations. Some examples are given below.

1. Field Due To An Infinitely Long Straight Uniformly Charged Wire:

Consider a thin infinitely long straight rod conductor having change density λ. (λ = \(\frac{q}{l}\))
To find the electric field at P, we imagine a Gaussian surface passing through P.
Then according to Gauss’s law we can write,

Integrating over the Gaussian surface, we get (we need not integrate the upper and lower surface because, electric lines do not pass through these surfaces.)

2. Field Due To A Uniformly Charged Infinite Plane Sheet

Consider an infinite thin plane sheet of change of density σ. To find electric field at a point P (at a distance ‘r’ from sheet), imagine a Gaussian surface in the form of cylinder having area of cross section ‘ds’.
According to Gauss’s law we can write,

(Since q = σds)
But electric field passes only through end surfaces ,so we get ∫ds = 2ds

E is directed away from the charged sheet, if a is positive and directed towards the sheet if a is negative.

3. Field Due To A Uniformly Charged Thin Spherical Shell: Consider a uniformly changed hollow spherical conductor of radius R. Let ‘q’ be the total charge on the surface.

To find the electric field at P (at a distance r from the centre), we imagine a Gaussian spherical surface having radius ‘r’.
Then, according to Gauss’s theorem we can write,

The electric field is constant, at a distance ‘r’. So we can write,

Case I: Electric field inside the shell is zero.
Case II: At the surface of shell r = R